The first transcendental functions we shall perform calculus operations on are the trig functions.
As we have seen, trigonometric functions are good at modelling periodic behavior.
The Derivative of $f(x)=\sin x$
| $y$ | | |
| $x$ |
The Derivative of $f(x)=\sin x$
$$\frac{d}{dx}\sin x=\cos x$$
The Derivative of $f(x)=\cos x$
| $y$ | | |
| $x$ |
The Derivative of $f(x)=\cos x$
$$\frac{d}{dx}\cos x=-\sin x$$
Example
Using the rules of derivatives we already have under our belts, find $$\frac{d}{dx}\tan x.$$
$$
\begin{array}{lll}
\displaystyle \frac{d}{dx}\tan x&=\displaystyle\frac{d}{dx}\frac{\sin x}{\cos x}&\\
&=\displaystyle\frac{(\cos x)(\sin x)'-(\sin x)(\cos x)'}{(\cos x)^2}&\mbox{ by the quotient rule}\\
&=\displaystyle\frac{(\cos x)(\cos x)-(\sin x)(-\sin x)}{\cos^2 x}&\\
&=\displaystyle\frac{\cos^2 x+\sin^2 x}{\cos^2 x}&\\
&=\displaystyle\frac{1}{\cos^2 x}& \mbox{by the Pythagorean Identity: $\sin^2 x + \cos^2 x = 1$}\\
&=\displaystyle \sec^2 x& \mbox{}\\
\end{array}
$$
The Other Three
In similar fashion, we can derive the following derivative formulas. $$\frac{d}{dx}\cot x = -\csc^2 x$$ $$\frac{d}{dx}\sec x=\sec x \tan x$$ $$\frac{d}{dx}\csc x = -\csc x \cot x$$
Example
Find $\displaystyle \frac{d^2 y}{dx^2}$ for the function $y=x\sin x-\cos x.$
Finding the first derivative:
$$
\begin{array}{lll}
\displaystyle \frac{dy}{dx}&=\displaystyle \frac{d}{dx}(x\sin x-\cos x)&\\
&=\displaystyle \frac{d}{dx}(x\sin x)-\frac{d}{dx}(\cos x)&\\
&=\displaystyle (x)'(\sin x)+(x)(\sin x)'-(-\sin x)&\mbox{by the product rule}\\
&=\displaystyle \sin x+x\cos x+\sin x&\\
&=\displaystyle 2\sin x+x\cos x&\\
\end{array}
$$
Finding the second derivative:
$$
\begin{array}{lll}
\displaystyle \frac{d^2y}{dx^2}&=\displaystyle \frac{d}{dx}(2\sin x+x\cos x)&\\
&=\displaystyle 2\frac{d}{dx}\sin x+\frac{d}{dx}(x\cos x)&\\
&=\displaystyle 2\cos x+(x)'(\cos x)+(x)(\cos x)'&\mbox{by the product rule}\\
&=\displaystyle 2\cos x+\cos x+x(-\sin x)&\\
&=\displaystyle 3\cos x-x\sin x&\\
\end{array}
$$
Example
Find $\displaystyle \frac{d^4 y}{dx^4 }$ for the function $y=4 \sin x$
$$
\begin{array}{lll}
\displaystyle \frac{dy}{dx}&=\displaystyle \frac{d}{dx}(4\sin x)&\\
&=\displaystyle 4\frac{d}{dx}\sin x&\\
&=\displaystyle 4\cos x&\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{d^2y}{dx^2}&=\displaystyle \frac{d}{dx}(4\cos x)&\\
&=\displaystyle 4\frac{d}{dx}\cos x&\\
&=\displaystyle 4(-\sin x)&\\
&=\displaystyle -4\sin x&\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{d^3y}{dx^3}&=\displaystyle \frac{d}{dx}(-4\sin x)&\\
&=\displaystyle -4\frac{d}{dx}\sin x&\\
&=\displaystyle -4\cos x&\\
\end{array}
$$
$$
\begin{array}{ll}
\displaystyle \frac{d^4y}{dx^4}&=\displaystyle \frac{d}{dx}(-4\cos x)&\\
&=\displaystyle -4\frac{d}{dx}\cos x&\\
&=\displaystyle -4(-\sin x)&\\
&=\displaystyle 4\sin x&\\
\end{array}
$$
Example
Find the equation of the tangent line to the function $f(x)= \sec x$ at $\displaystyle x=-\frac{\pi}{4}$
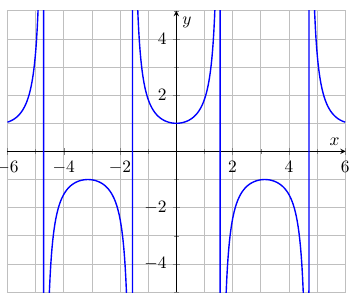
First we find the derivative of $\sec x:$
$$
\begin{array}{ll}
\displaystyle f'(x)&=\displaystyle \frac{d}{dx} \sec x&\\
&=\displaystyle \sec x \tan x&\\
\end{array}
$$
Thus, the slope of our tangent line is
$$
\begin{array}{ll}
\displaystyle f'\left(-\frac{\pi}{4}\right)&=\displaystyle \sec\left(-\frac{\pi}{4}\right) \tan\left(-\frac{\pi}{4}\right)&\\
&=\displaystyle \frac{2}{\sqrt{2}}\cdot (-1)&\\
&=\displaystyle -\frac{2}{\sqrt{2}}&\\
&=\displaystyle -\sqrt{2}& \mbox{rationalizing denominator}\\
\end{array}
$$
Now $\displaystyle f\left(-\frac{\pi}{4}\right)=\frac{2}{\sqrt{2}}=\sqrt{2}.$ Then,
$$
\begin{array}{ll}
\displaystyle y-f(a)=f'(a)(x-a)&\\
\implies \displaystyle y-f\left(-\frac{\pi}{4}\right)=f'\left(-\frac{\pi}{4}\right)\left(x-\left(-\frac{\pi}{4}\right)\right)&\\
\implies \displaystyle y-\sqrt{2}=-\sqrt{2}\left(x+\frac{\pi}{4}\right)&\\
\end{array}
$$
is our tangent line.
Putting the above into slope-intercept form: $$ \begin{array}{ll} \displaystyle y-\sqrt{2}=-\sqrt{2}\left(x+\frac{\pi}{4}\right)&\\ \implies \displaystyle y-\sqrt{2}=(-\sqrt{2})x-\sqrt{2}\frac{\pi}{4}&\\ \implies \displaystyle y=(-\sqrt{2})x-\sqrt{2}\frac{\pi}{4}+\sqrt{2}&\\ \implies \displaystyle y=(-\sqrt{2})x+\frac{(4-\pi)\sqrt{2}}{4}&\\ \end{array} $$
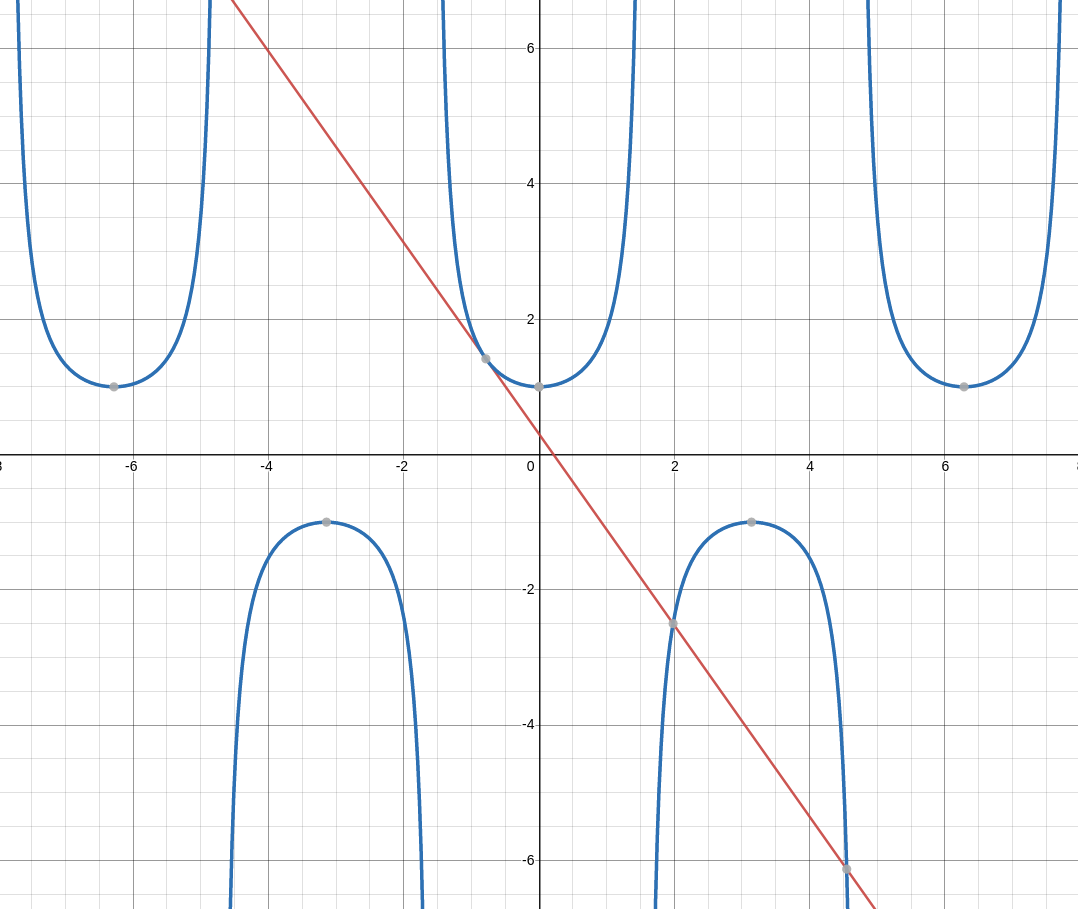
Putting the above into slope-intercept form: $$ \begin{array}{ll} \displaystyle y-\sqrt{2}=-\sqrt{2}\left(x+\frac{\pi}{4}\right)&\\ \implies \displaystyle y-\sqrt{2}=(-\sqrt{2})x-\sqrt{2}\frac{\pi}{4}&\\ \implies \displaystyle y=(-\sqrt{2})x-\sqrt{2}\frac{\pi}{4}+\sqrt{2}&\\ \implies \displaystyle y=(-\sqrt{2})x+\frac{(4-\pi)\sqrt{2}}{4}&\\ \end{array} $$

Application
Let the position of a mass in an undamped spring–mass system in simple harmonic motion be given by $s(t)=a\cos t +b\sin t.$
(a) Find the constants $a$ and $b$ such that when the velocity is $3 \mbox{ cm/s},$ the position is $s=0,$ and when $t=0.$
From the above information, we may write two equations: $s'(0)=3$ and $s(0)=0.$
Now, $s(0)=0$ gives that $a\cos 0 +b\sin 0=0,$ which becomes $a=0.$
Thus, our position function has the form $s(t)=b\sin t$ and our velocity function has the form $s'(t)=b\cos t$
Since $s'(0)=3,$ we have the equation $b\cos 0 = 3,$ or simply $b=0.$
Our position function is then $s(t)=3\sin t.$ That is, the constants we seek are $a=0$ and $b=3.$
Now, $s(0)=0$ gives that $a\cos 0 +b\sin 0=0,$ which becomes $a=0.$
Thus, our position function has the form $s(t)=b\sin t$ and our velocity function has the form $s'(t)=b\cos t$
Since $s'(0)=3,$ we have the equation $b\cos 0 = 3,$ or simply $b=0.$
Our position function is then $s(t)=3\sin t.$ That is, the constants we seek are $a=0$ and $b=3.$
(b) Over which interval(s) is the velocity positive?
From the above, the velocity is positive when $s'(t) \gt 0.$
That is, when $3 \cos t \gt 0,$ or more simply, when $\cos t \gt 0.$
Now, in general, $\cos t$ is positive when $\displaystyle -\frac{\pi}{2}+2k\pi \lt t \lt \frac{\pi}{2}+2k\pi$ where $k \in \mathbb{Z}$ ($k$ is an integer).
But since we are measuring from $t=0,$ the velocity is positive on the interval $\displaystyle \left(0,\frac{\pi}{2}\right)$ and the intervals $\displaystyle \left(-\frac{\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right)$ where $k \in \mathbb{N}$ ($k$ is a positive integer).
That is, when $3 \cos t \gt 0,$ or more simply, when $\cos t \gt 0.$
Now, in general, $\cos t$ is positive when $\displaystyle -\frac{\pi}{2}+2k\pi \lt t \lt \frac{\pi}{2}+2k\pi$ where $k \in \mathbb{Z}$ ($k$ is an integer).
But since we are measuring from $t=0,$ the velocity is positive on the interval $\displaystyle \left(0,\frac{\pi}{2}\right)$ and the intervals $\displaystyle \left(-\frac{\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right)$ where $k \in \mathbb{N}$ ($k$ is a positive integer).