Derivatives tell us the slope of the tangent line of a curve at a point.
The slope of the tangent line is the instantaneous rate of change of the vertical with respect to the horizontal.
Today we're going to explore rates of change a bit more by expanding our list of applications. We're also going to begin interpreting the meaning of the second derivative.
The Derivative as a Rate of Change
Recall: To interpret a slope (i.e., a derivative!), remember $$\mbox{units of derivative}=\mbox{units of slope}=\frac{\mbox{vertical units}}{\mbox{horizontal units}}$$
Recall: Average Rate of Change of a Function
The average rate of change of $f(x)$ over the interval $[a,a+h]$ is $\displaystyle \frac{f(a+h)-f(a)}{h}.$
Recall: Instantaneous Rate of Change
The instantaneous rate of change of $f(x)$ at $x=a,$ is $\displaystyle f'(a).$
This is because $f'(a)$ is the limiting value of the difference quotient $\displaystyle \frac{f(a+h)-f(a)}{h}$ as $h \rightarrow 0.$
Recall: Velocity is the rate at which an object's position changes with respect to time.
Suppose we have a function which gives an object's distance in meters with respect to time in seconds, say $s(t).$
Then $s'(t)$ is the velocity of the object.
Recall the Example: Velocity
Using propane, ethanol, methanol and butane, a potato cannon produce muzzle velocities of between $28$ and $48$ meters per second. (Source: U.S. Air Force Measures Potato Cannon Muzzle Velocities).
Suppose the muzzle velocity of a potato cannon is $32$ m/s and that the downward acceleration due to gravity is $9.8$ m/s2. Then, when fired vertically, the height $s$ in meters of the potato above the ground $t$ seconds after firing can be expressed (ignoring air resistance) as $s(t)=-4.9t^2+32t.$
What is the velocity of the potato $2$ seconds after firing?

Recall: Average Versus Instantaneous Velocity
Consider the equation $s(t)=-4.9t^2+32t$ of the height of our potato with respect to time. The instantaneous velocity of the potato at $t=2$ seconds is $s'(2)=12.4$ m/s
Rates of Change
Suppose we have a function which gives an object's distance in meters with respect to time in seconds, say $s(t).$
We have learned that the meaning of $s'(t)$ is the velocity of the object.
What is the meaning of $s''(t)?$
Hint: What are its units?
Acceleration is the rate at which an object's velocity changes with respect to time.
Suppose we have a function which gives an object's distance in meters with respect to time in seconds, say $s(t).$
The velocity is given by the function $v(t)=s'(t),$ thus, $v'(t)=s''(t)$ is the rate at which of the object's velocity is changing.
That is to say that $s''(t)$ is the acceleration of the object.
Acceleration
We can also think of acceleration as the speed at which a speedometer needle moves.

Example: Acceleration
Using propane, ethanol, methanol and butane, a potato cannon produce muzzle velocities of between $28$ and $48$ meters per second. (Source: U.S. Air Force Measures Potato Cannon Muzzle Velocities).
Suppose the muzzle velocity of a potato cannon is $32$ m/s and that the downward acceleration due to gravity is $9.8$ m/s2. Then, when fired vertically, the height $s$ in meters of the potato above the ground $t$ seconds after firing can be expressed (ignoring air resistance) as $s(t)=-4.9t^2+32t.$
What is the acceleration of the potato $2$ seconds after firing?

Last time we saw that
$$
v(t)=s'(t)=-9.8t+32.
$$
Thus,
$$
a(t)=s''(t)=-9.8.
$$
That is, the acceleration is a constant $-9.8$ $\mbox{m}/\mbox{s}^2$ at at time $t.$
So, $2$ second after firing, the acceleration of the potato is $-9.8$ $\mbox{m}/\mbox{s}^2.$
We can interpret the above to mean that every second the potato is in the air, it loses $9.8$ $\mbox{m}/\mbox{s}$ of velocity.
So, $2$ second after firing, the acceleration of the potato is $-9.8$ $\mbox{m}/\mbox{s}^2.$
We can interpret the above to mean that every second the potato is in the air, it loses $9.8$ $\mbox{m}/\mbox{s}$ of velocity.
Example
The function $s(t)=2t^3 - 15t^2 + 36t - 10$ represents the position of a particle travelling along a horizontal line.
a. Find the velocity and acceleration functions.
The velocity function is the first derivative $v(t)=s'(t)=6t^2-30t+36.$
The acceleration function is the second derivative $a(t)=s''(t)=12t-30.$
The acceleration function is the second derivative $a(t)=s''(t)=12t-30.$
b. Determine the time intervals when the object is moving backward (negative velocity) or moving forward (positive velocity).
We must determine where the velocity is negative and where it's positive.
We first factor the derivative to find points where the velocity (derivative) is $0.$
These are the points where the sign of the velocity (derivative) can change.
$$
\begin{array}{l}
v(t)=s'(t)=6t^2-30t+36=0\\
\implies 6(t^2-5t+6)=0\\
\implies 6(t-2)(t-3)=0\\
\implies t-2=0 \mbox{ OR } t-3=0\\
\implies t=2 \mbox{ OR } t=3\\
\end{array}
$$
Thus, the velocity is $0$ at $t=2$ seconds and $t=3$ seconds. These are the places where the velocity can change sign.
From the above we may create a sign diagram:

From the above sign diagram for the velocity function (derivative), we see that the velocity (derivative) is negative on the interval $(2,3).$ That is, the object is moving backward on the time interval $(2,3).$
We also see that that the velocity (derivative) is positive on the interval $[0,2)\cup(3,\infty).$ That is, the object is moving forward on the time interval $[0,2)\cup(3,\infty).$
From the above we may create a sign diagram:

From the above sign diagram for the velocity function (derivative), we see that the velocity (derivative) is negative on the interval $(2,3).$ That is, the object is moving backward on the time interval $(2,3).$
We also see that that the velocity (derivative) is positive on the interval $[0,2)\cup(3,\infty).$ That is, the object is moving forward on the time interval $[0,2)\cup(3,\infty).$
c. Determine the time intervals when the object is:
- slowing down (velocity and acceleration have opposite signs)
- speeding up (velocity and acceleration have the same sign).
To determine where the velocity and acceleration have opposite signs, we need to make a sign diagram for the acceleration as well.
To do so, we determine where the acceleration (second derivative) is $0:$
$$
\begin{array}{l}
a(t)=s''(t)=12t-30=0\\
\implies 6(2t-5)=0\\
\implies 2t-5=0\\
\implies t=\displaystyle \frac{5}{2}=2.5.\\
\end{array}
$$
The acceleration (second derivative) is $0$ at $t=2.5$ seconds. Now, the acceleration $a(t)=s''(t)=2t-5$ is positive when $t \gt 2.5,$
and negative when $t \lt 2.5.$ We may now make the sign diagram for acceleration (second derivative):

To determine where the the signs are the same and where they differ, we put these two diagrams together:
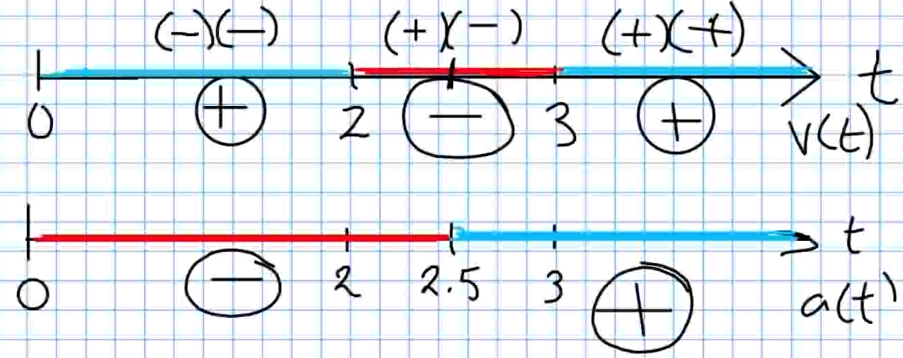
Thus, we see that the signs differ on the interval $(0,2)\cup (2.5,3)$ and are the same on the interval $(2,2.5)\cup(3,\infty).$
We conclude that the object is slowing down on the time interval $(0,2)\cup (2.5,3)$ and is speeding up on the time interval $(2,2.5)\cup(3,\infty).$

To determine where the the signs are the same and where they differ, we put these two diagrams together:

Thus, we see that the signs differ on the interval $(0,2)\cup (2.5,3)$ and are the same on the interval $(2,2.5)\cup(3,\infty).$
We conclude that the object is slowing down on the time interval $(0,2)\cup (2.5,3)$ and is speeding up on the time interval $(2,2.5)\cup(3,\infty).$
Example: The following graph shows the position $y = s(t)$ of an object moving along a straight line.

The velocity is positive, negative, or zero when the derivative is positive, negative, or zero.
Thus, from the graph we see that:
The velocity is positive on the time interval $(0,1.5)\cup(6,7).$
The velocity is negative on the time interval $(1.5,2)\cup(5,6).$
The velocity is zero on the set $\{1.5\}\cup(2,5)\cup\{6\}.$
Thus, from the graph we see that:
The velocity is positive on the time interval $(0,1.5)\cup(6,7).$
The velocity is negative on the time interval $(1.5,2)\cup(5,6).$
The velocity is zero on the set $\{1.5\}\cup(2,5)\cup\{6\}.$
b. Sketch the graph of the velocity function.
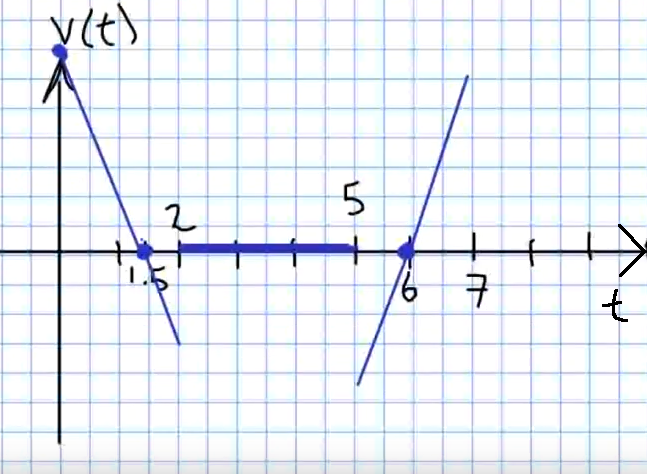
c. Use the graph of the velocity function to determine the time intervals when the acceleration is positive, negative, or zero.
The slope of the velocity graph gives the acceleration. Thus, from the above graph:
The acceleration is positive on the time interval $(5,7).$
The acceleration is negative on the time interval $(0,2).$
The acceleration is zero on the time interval $(2,5).$
The acceleration is positive on the time interval $(5,7).$
The acceleration is negative on the time interval $(0,2).$
The acceleration is zero on the time interval $(2,5).$
d. Determine the time intervals when the object is speeding up or slowing down.
From the above information we can make a sign diagram for both $v(t)$ and $a(t):$
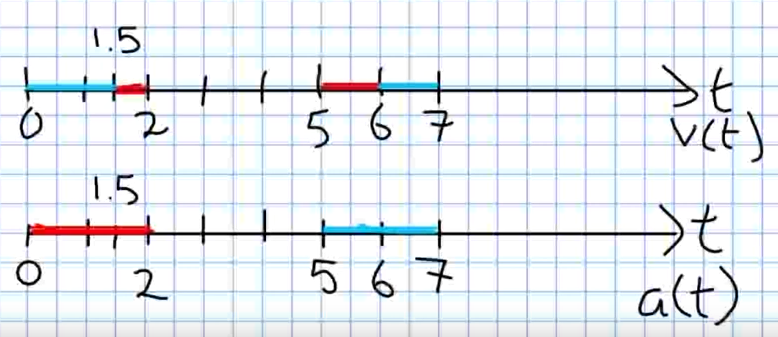
From the above sign diagrams we see that, we see that the object is speeding up on $(1.5,2)\cup(6,7)$ and is slowing down on $(0,1.5)\cup(5,6).$

From the above sign diagrams we see that, we see that the object is speeding up on $(1.5,2)\cup(6,7)$ and is slowing down on $(0,1.5)\cup(5,6).$
Recovering the Change in a Function from its Rate of Change
Suppose you're on I-5 heading up to Portland.
You set the cruise control to $65$ mph. How far have you gone after $2$ hours?

Recovering the Change in a Function from its Rate of Change
Using techniques of calculus, we can recover the total change in a quantity from its rate of change even when the rate of change varies.
Estimating the Change in a Function: For small values of $h,$ the difference quotient is approximately equal to the derivative: $$\frac{f(a+h)-f(a)}{h}\approx f'(a).$$ Consequently, $$f(a+h)-f(a)\approx f'(a) \cdot h.$$ This enables us to estimate how much a function has changed given only a function value and its derivative at $x=a.$
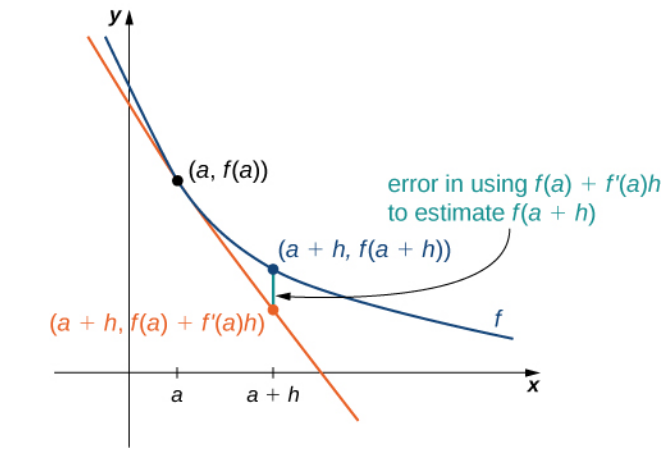
Example: Estimating the Change in a Function
(a) Find the exact change in $f(x)=x^2$ when $x$ is increased from $1$ to $1.2.$
(b) Estimate the change in $f(x)=x^2$ when $x$ is increased from $1$ to $1.2.$
(a) The exact change is $f(1.2)-f(1)=1.2^2-1^2=1.44-1=0.44.$
(b) Since $f(a+h)-f(a)\approx f'(a) \cdot h,$ we may estimate the change in $f$ as $$f(1.2)-f(1)=f(1+0.2)-f(1)\approx f'(1) \cdot 0.2=2 \cdot 0.2=0.4.$$
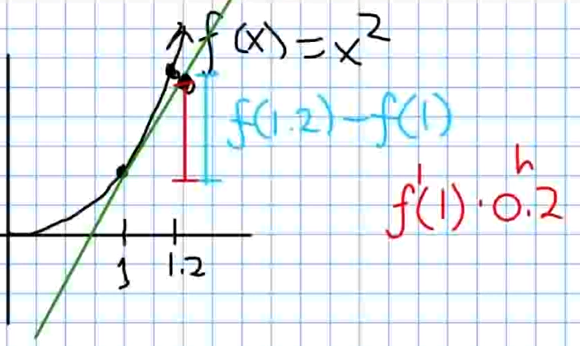
(b) Since $f(a+h)-f(a)\approx f'(a) \cdot h,$ we may estimate the change in $f$ as $$f(1.2)-f(1)=f(1+0.2)-f(1)\approx f'(1) \cdot 0.2=2 \cdot 0.2=0.4.$$
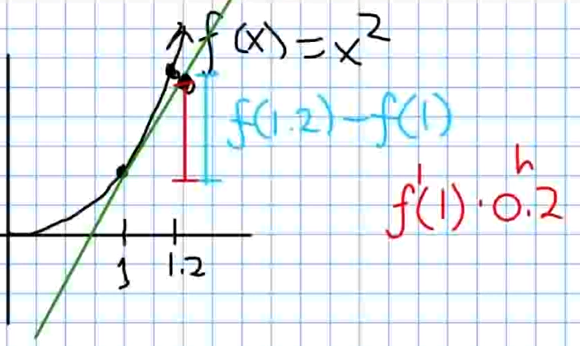
Example: Estimating the Change in a Function
Let $f(t)$ be the amount of a drug of injected into the bloodstream that remains $t$ hours after the injection. If the amount of the drug in the bloodstream after $3$ hours is $7$ milligrams, and is being metabolized at a rate of $0.55$ milligrams per hour, estimate the amount of the drug remaining in the bloodstream after $3.8$ hours.
To find the amount of the drug in the bloodstream after $3.8$ hours, we will first estimate the change in concentration
of the drug over the time period between $3$ hours and $3.8$ hours, that is $f(3.8)-f(3).$ Taking $h=0.8$ we have:
$$f(3.8)-f(3)=f(3+0.8)-f(3) \approx f'(3) \cdot 0.8 = -0.55 \cdot 0.8 =-0.44.$$
Thus, from $t=3$ hours to $t=3.8,$ about $0.44$ milligrams of the drug is metabolized.
We conclude that at $t=3.8$ hours there is about $6.56$ milligrams of the drug remaining.
We conclude that at $t=3.8$ hours there is about $6.56$ milligrams of the drug remaining.
Marginal Cost
The marginal cost in producing an item is the increase or decrease in cost that occurs when we produce one more unit.
For example, suppose we are manufacturing some good (like radios, whiskey, umbrellas, etc.) and at the present moment we are producing $1000$ units every day.
In this situation, the marginal cost is the change in our cost when we scale up production to $1001$ units.
Marginal Cost
Let $C(x)$ be a cost function for producing $x$ items.
For small values of $h,$ the difference quotient is approximately equal to the derivative: $$\frac{C(a+h)-C(a)}{h}\approx C'(a).$$ Consequently, $$C(a+h)-C(a)\approx C'(a) \cdot h.$$
Taking $h=1$ gives us an approximation for the marginal cost: $$C(a+1)-C(a) \approx C'(a).$$
In economics, $C'(x)$ is called the marginal cost function since it approximates the marginal cost at any value of $x.$
The following give approximations for the marginal cost, marginal revenue, and marginal profit: $$C(a+1)-C(a) \approx C'(a).$$ $$R(a+1)-R(a) \approx R'(a).$$ $$P(a+1)-P(a) \approx P'(a).$$
Example: Marginal Profit
A profit is earned when revenue exceeds cost. Suppose the profit function for a skateboard manufacturer is given by $P(x) = 30x - 0.3x^2 - 250,$ where $x$ is the number of skateboards sold.
a. Find the exact profit from the sale of the thirty first skateboard.
Computation for the exact profit from the sale of the $31$st skateboard:
$$f(31)-f(30)=391.70-380=11.70.$$
The exact profit is $\$11.70.$
b. Find the marginal profit function and use it to estimate the profit from the sale of the thirty first skateboard.
The marginal profit function is $P'(x) = 30 - 0.6x.$
Thus, we may now estimate the profit from the $31$st skateboard:
$$f(31)-f(30)\approx f'(30) = 30-0.6\cdot 30 =12.$$
The estimated profit is $\$12.$
Other Rates of Change: Population Growth
The population of Oregon can be modelled by the function $P(t)=150.5666t^2-536.9966t +51539.7709$ where $t$ is measured in years since $1850.$
In the graph below the blue dots are census data and the red curve is $P(t).$
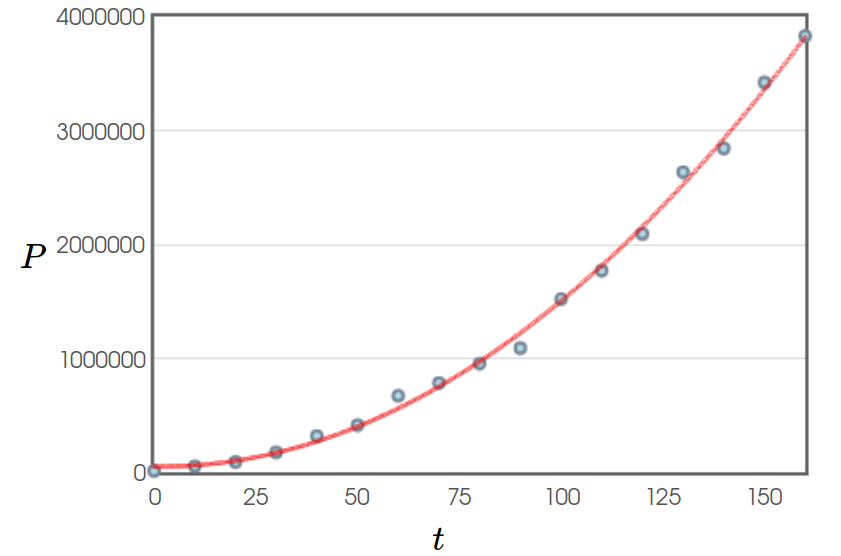
$$P'(t)=301.1332t-536.9966$$
b. Find $P'(170)$ Interpret what the result means for the state of Oregon.
$$P'(170)=301.1332 \cdot 170-536.9966 \approx 50656$$
That is, in $2020,$ Oregon was growing at a rate of about $\mbox{50,656}$ people per year.
c. Find $P''(170)$ Interpret what the result means for the state of Oregon.
$
P''(x)=301.1332,
$
so $P''(170) \approx 301.$
We interpret this to mean that in $2020,$ the rate at which Oregon's population was increasing per year was itself increasing by about $301$ people per year.
We interpret this to mean that in $2020,$ the rate at which Oregon's population was increasing per year was itself increasing by about $301$ people per year.