As cuddly and lovable as our definition of the derivative is, $$f'(x)=\lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h},$$ using it can be quite cumbersome, as you likely already know.
In this section we learn some shortcuts to finding derivatives that will enable us to find derivatives quickly.
Pop Quiz #1: If $f(x)=x,$ what is $f'(x)?$
$$
f'(x)=1
$$
$$
f'(x)=0
$$
Derivatives of Linear and Constant Functions
Linear: If $f(x)=x,$ then $f'(x)=1$
Constant: If $f(x)=c$ where $c$ is a constant, then $f'(x)=0.$
The above may also be written as $$\frac{d}{dx}x=1$$ $$\frac{d}{dx}c=0$$
Recall: The slope of a function at a point is itself a function called the derivative and is denoted $\displaystyle \frac{dy}{dx}=f'(x).$
Example: The derivative of $\displaystyle f(x)=\frac{1}{x}=x^{-1}$ is $\displaystyle f'(x)=-\frac{1}{x^2}=-x^{-2}.$
Example: The derivative of $f(x)=x^2$ is $f'(x)=2x.$
Example: The derivative of $f(x)=x^3$ is $???$
Generally Speaking $$ \begin{array}{c|c} \hline \mbox{Function} & \mbox{Derivative} \\ \hline f(x)=x^{-1} & f'(x)=-x^{-2}\\ \hline f(x)=c & f'(x)=0\\ \hline f(x)=x & f'(x)=1 \\ \hline f(x)=x^2 & f'(x)=2x \\ \hline f(x)=x^3 & f'(x)=3x^2 \\ \hline f(x)=x^4 & f'(x)= \\ \hline \vdots & \vdots \\ \hline f(x)=x^n & f'(x)= \\ \hline \end{array} $$
The Power Rule
For any integer $n$, the derivative of $f(x)=x^n$ is $$f'(x)=nx^{n-1}.$$
We may also write this rule as $$\frac{d}{dx}x^n=nx^{n-1}.$$
The Power Rule
For any integer $n,$ the derivative of $f(x)=x^n$ is $f'(x)=nx^{n-1}.$
Example: Find the derivative of $f(x)=x^5.$
$$
f'(x)=5x^4
$$
Example: Find the derivative of $f(x)=x^{-5}.$
$$
f'(x)=-5x^{-6}
$$
More Differentiation Rules
Constant Multiple: $\displaystyle \frac{d}{dx}\left[ k \cdot f(x)\right]=k \cdot \frac{d}{dx} f(x)$
Sum Rule: $\displaystyle \frac{d}{dx}\left[ f(x)+g(x) \right]=\frac{d}{dx} f(x)+ \frac{d}{dx} g(x)$
Difference Rule: $\displaystyle \frac{d}{dx}\left[ f(x)-g(x) \right]=\frac{d}{dx} f(x)- \frac{d}{dx} g(x)$
Constant Multiple: $\displaystyle \frac{d}{dx}\left[ k \cdot f(x)\right]=k \cdot \frac{d}{dx} f(x)$
Example: $\displaystyle \frac{d}{dx} \left(2 x^3\right)$
$$
\begin{array}{lll}
\displaystyle \frac{d}{dx} \left(2 x^3\right)&=\displaystyle 2 \frac{d}{dx} x^3 & \mbox{the derivative of a constant multiple is a constant multiple of the derivatives}\\
&=\displaystyle 2 (3x^2)& \mbox{by the power rule}\\
&=\displaystyle 6x^2 & \mbox{}\\
\end{array}
$$
Sum/Difference Rule: $\displaystyle \frac{d}{dx}\left[ f(x) \pm g(x) \right]=\frac{d}{dx} f(x) \pm \frac{d}{dx} g(x)$
Example: $\displaystyle \frac{d}{dx} \left(2x^3- 6x^2+ 3\right)$
$$
\begin{array}{lll}
\displaystyle \frac{d}{dx} \left(2x^3- 6x^2+ 3\right)&=\displaystyle \frac{d}{dx}(2x^3)- \frac{d}{dx}(6x^2)+ \frac{d}{dx}3&\mbox{the derivative of a sum/difference is the sum/difference of the derivatives}\\
&=\displaystyle 2\frac{d}{dx}x^3- 6\frac{d}{dx}x^2+ 0&\mbox{the derivative of a constant multiple is a constant multiple of the derivatives}\\
&=\displaystyle 2(3x^2)- 6(2x)&\mbox{by the power rule}\\
&=\displaystyle 6x^2- 12x&\mbox{}\\
\end{array}
$$
Example: $\displaystyle \frac{d}{dx} \left(\frac{4}{x^2}+\frac{1}{3x^3}\right)$
$$
\begin{array}{lll}
\displaystyle \frac{d}{dx} \left(\frac{4}{x^2}+\frac{1}{3x^3}\right)&=\displaystyle \frac{d}{dx}\frac{4}{x^2}+\frac{d}{dx}\frac{1}{3x^3}&\mbox{the derivative of a sum is the sum of the derivatives}\\
&=\displaystyle \frac{d}{dx}(4x^{-2})+\frac{d}{dx}\left(\frac{1}{3}x^{-3}\right)&\mbox{rewrite to set up for power rule}\\
&=\displaystyle 4\frac{d}{dx}x^{-2}+\frac{1}{3}\frac{d}{dx}x^{-3}&\mbox{the derivative of a constant multiple is a constant multiple of the derivatives}\\
&=\displaystyle 4(-2x^{-3})+\frac{1}{3}(-3x^{-4})&\mbox{by the power rule}\\
&=\displaystyle -8x^{-3}-x^{-4}&\mbox{}\\
&=\displaystyle -\frac{8}{x^3}-\frac{1}{x^{4}}&\mbox{optional step of rewriting with positive exponents}\\
\end{array}
$$
With the rules we've learned so far, we can now differentiate (find the derivative of) any polynomial.
The fun doesn't stop there though, there are many different classes of functions which we will be covering.
Moreover, we've covered the operations of sum and difference. We now move into products and quotients.
The Product Rule
$$\frac{d}{dx}[f(x)g(x)]=f'(x)g(x)+g'(x)f(x)$$
Example
Find the derivative of the function $\displaystyle p(x)=2x^5(4x^2+x)$ in two ways:
1) by distributing and then taking a derivative, and
2) by using the product rule.
| Method 1 | Method 2 | |
| $$ \begin{array}{ll} \displaystyle \frac{d}{dx} \left(2x^5(4x^2+x)\right)&\mbox{}\\ =\displaystyle \frac{d}{dx} \left(8x^7+2x^6\right)&\mbox{}\\ =\displaystyle \frac{d}{dx}(8x^7)+\frac{d}{dx}(2x^6)&\mbox{}\\ =\displaystyle 8\frac{d}{dx}x^7+8\frac{d}{dx}x^6&\mbox{}\\ =\displaystyle 8(7x^6)+2(6x^5)&\mbox{}\\ =\displaystyle 56x^6+12x^5&\mbox{}\\ \end{array} $$ | $$ \begin{array}{ll} \displaystyle \frac{d}{dx} \left(2x^5(4x^2+x)\right)&\mbox{}\\ =f'(x)g(x)+g'(x)f(x)&\\ =\displaystyle (2x^5)'(4x^2+x)+(4x^2+x)'(2x^5) &\mbox{}\\ =\displaystyle (10x^4)(4x^2+x)+(8x+1)(2x^5) &\mbox{}\\ =\displaystyle 40x^6+10x^5+16x^6+2x^5 &\mbox{}\\ =\displaystyle 56x^6+12x^5 &\mbox{}\\ \end{array} $$ |
At this point you might be thinking, "why learn another rule when we can just multiply?"
Here's why...
Example
Find the derivative of the following function $$\displaystyle F(x)=\left(2x^3- 6x^2+5x+ 3\right)\left(\frac{4}{x^2}+\frac{1}{3x^3}\right).$$ A Wee Bit of Advice:
- Identify $f$ and $g.$
- Then find $f'$ and $g'$.
- Finally substitute everything into the product rule.
1) Take $f(x)=2x^3- 6x^2+5x+ 3$ and $\displaystyle g(x)=\frac{4}{x^2}+\frac{1}{3x^2}.$
2) Then, $f'(x)=6x^2-12x+5$ and $\displaystyle g'(x)=-\frac{8}{x^3}-\frac{1}{x^{4}}.$ (found in a previous example)
3) Now use the product rule: $$ \begin{array}{ll} \displaystyle \frac{d}{dx} \left( \left(2x^3- 6x^2+5x+ 3\right)\left(\frac{4}{x^2}+\frac{1}{3x^3}\right) \right)&\\ =\displaystyle f'(x)g(x)+g'(x)f(x)&\\ =\displaystyle \left(6x^2-12x+5\right)\left(\frac{4}{x^2}+\frac{1}{3x^2}\right)+\left(-\frac{8}{x^3}-\frac{1}{x^{4}}\right)\left(2x^3- 6x^2+5x+ 3\right)& \mbox{}\\ =\displaystyle \left(6x^2-12x+5\right)\left(\frac{4}{x^2}+\frac{1}{3x^2}\right)-\left(\frac{8}{x^3}+\frac{1}{x^{4}}\right)\left(2x^3- 6x^2+5x+ 3\right)& \mbox{reasonably simplify}\\ \end{array} $$ There's a point when "simplifying" doesn't make things simpler. The above is one such case. It's fine to leave the above in unmultiplied form.
2) Then, $f'(x)=6x^2-12x+5$ and $\displaystyle g'(x)=-\frac{8}{x^3}-\frac{1}{x^{4}}.$ (found in a previous example)
3) Now use the product rule: $$ \begin{array}{ll} \displaystyle \frac{d}{dx} \left( \left(2x^3- 6x^2+5x+ 3\right)\left(\frac{4}{x^2}+\frac{1}{3x^3}\right) \right)&\\ =\displaystyle f'(x)g(x)+g'(x)f(x)&\\ =\displaystyle \left(6x^2-12x+5\right)\left(\frac{4}{x^2}+\frac{1}{3x^2}\right)+\left(-\frac{8}{x^3}-\frac{1}{x^{4}}\right)\left(2x^3- 6x^2+5x+ 3\right)& \mbox{}\\ =\displaystyle \left(6x^2-12x+5\right)\left(\frac{4}{x^2}+\frac{1}{3x^2}\right)-\left(\frac{8}{x^3}+\frac{1}{x^{4}}\right)\left(2x^3- 6x^2+5x+ 3\right)& \mbox{reasonably simplify}\\ \end{array} $$ There's a point when "simplifying" doesn't make things simpler. The above is one such case. It's fine to leave the above in unmultiplied form.
Dire Warning #1
WHEN YOU DO THIS
$\displaystyle \frac{d}{dx}[f(x)g(x)]=\frac{d}{dx}f(x)\cdot \frac{d}{dx}g(x)$
YOU MAKE KITTY ANGRY!!!!!!!!!!!!!!!!!!


The Quotient Rule
$$\frac{d}{dx}\left[\frac{f(x)}{g(x)}\right]=\frac{f'(x)g(x)-g'(x)f(x)}{[g(x)]^2}$$
Another Way To Remember...
$$\frac{d}{dx}\left[\frac{f(x)}{g(x)}\right]=\frac{g(x)f'(x)-f(x)g'(x)}{[g(x)]^2}$$ The above may be read as:
Low d high minus high d low, over the square of the low.
Example
Differentiate the function $$\displaystyle s(t)=\frac{t^4+1}{t^4-1}.$$ A Wee Bit of Advice:
- Identify $f$ and $g.$
- Then find $f'$ and $g'$.
- Finally substitute everything into the quotient rule.
1) Take $f(t)=t^4+1$ and $\displaystyle g(t)=t^4-1.$
2) Then, $f'(t)=4t^3$ and $\displaystyle g'(t)=4t^3.$
3) Now use the quotient rule: $$ \begin{array}{lll} \displaystyle \frac{d}{dt} \frac{t^4+1}{t^4-1}&=\displaystyle \frac{g(t)f'(t)-f(t)g'(t)}{[g(t)]^2}&\\ &=\displaystyle \frac{(t^4-1)(4t^3)-(t^4+1)(4t^3)}{(t^4-1)^2}&\\ &=\displaystyle \frac{4t^7-4t^3-(4t^7+4t^3)}{(t^4-1)^2}&\\ &=\displaystyle \frac{4t^7-4t^3-4t^7-4t^3}{(t^4-1)^2}&\\ &=\displaystyle -\frac{8t^3}{(t^4-1)^2}&\\ \end{array} $$
2) Then, $f'(t)=4t^3$ and $\displaystyle g'(t)=4t^3.$
3) Now use the quotient rule: $$ \begin{array}{lll} \displaystyle \frac{d}{dt} \frac{t^4+1}{t^4-1}&=\displaystyle \frac{g(t)f'(t)-f(t)g'(t)}{[g(t)]^2}&\\ &=\displaystyle \frac{(t^4-1)(4t^3)-(t^4+1)(4t^3)}{(t^4-1)^2}&\\ &=\displaystyle \frac{4t^7-4t^3-(4t^7+4t^3)}{(t^4-1)^2}&\\ &=\displaystyle \frac{4t^7-4t^3-4t^7-4t^3}{(t^4-1)^2}&\\ &=\displaystyle -\frac{8t^3}{(t^4-1)^2}&\\ \end{array} $$
Oh! And let's not forget, let's NOT forget that...
Dire Warning #2
WHEN YOU DO THIS
$\displaystyle \frac{d}{dx}\frac{f(x)}{g(x)}=\frac{\frac{d}{dx}f(x)}{\frac{d}{dx}g(x)}$
YOU MAKE KITTY ANGRY!!!!!!!!!!!!!!!!!!


Example
Assume that $f(x)$ and $g(x)$ are both differentiable functions with values as given in the following table.

Use the table to calculate $h'(1)$ if $\displaystyle h(x) = x f (x) + \frac{g(x)}{4 f(x)}.$
$$
\begin{array}{lll}
h'(x)&=\displaystyle \frac{d}{dx} \left(x f (x) + \frac{g(x)}{4 f(x)}\right)&\mbox{}\\
&=\displaystyle \frac{d}{dx}(x f (x)) + \frac{d}{dx}\frac{g(x)}{4 f(x)}&\mbox{}\\
&=\displaystyle (x)'f (x)+f'(x)\cdot x + \frac{4 f(x)g'(x)-g(x)\cdot 4f'(x)}{(4 f(x))^2}&\mbox{}\\
&=\displaystyle f (x)+xf'(x) + \frac{4 f(x)g'(x)-4g(x)f'(x)}{16 f(x)^2}&\mbox{}\\
\end{array}
$$
Thus, using the above along with our table $(f(1)=3, g(1)=2, f'(1)=-1,$ and $g'(1)=4),$
$$
\begin{array}{lll}
h'(1)&=\displaystyle f (1)+1 \cdot f'(1) + \frac{4 f(1)g'(1)-4g(1)f'(1)}{16 f(1)^2}&\mbox{}\\
&=\displaystyle 3+1\cdot (-1) + \frac{4 \cdot 3 \cdot 4-4\cdot 2\cdot (-1)}{16 (3)^2}&\mbox{}\\
&=\displaystyle 2 + \frac{56}{144}&\mbox{}\\
&=\displaystyle 2 + \frac{7}{18}&\mbox{}\\
&=\displaystyle \frac{43}{18}&\mbox{}\\
&=2.3\overline{8}
\end{array}
$$
Application: Velocity
Using propane, ethanol, methanol and butane, a potato cannon produce muzzle velocities of between $28$ and $48$ meters per second. (Source: U.S. Air Force Measures Potato Cannon Muzzle Velocities).
Suppose the muzzle velocity of a potato cannon is $32$ m/s and that the downward acceleration due to gravity is $9.8$ m/s2. Then, when fired vertically, the height $s$ in meters of the potato above the ground $t$ seconds after firing can be expressed (ignoring air resistance) as $s(t)=-4.9t^2+32t.$
What is the velocity of the potato $2$ seconds after firing?

The velocity of the potato after $2$ seconds is given by $s'(2).$
Since $s'(t)=-9.8t+32,$ we have that $s'(2)=-9.8\cdot 2+32=12.4.$
Thus, the velocity of the potato $2$ seconds after firing is $12.4$ meters per second.
Since $s'(t)=-9.8t+32,$ we have that $s'(2)=-9.8\cdot 2+32=12.4.$
Thus, the velocity of the potato $2$ seconds after firing is $12.4$ meters per second.
Application: Timber Yield
The relationship between the age $t$ of a stand of trees and the yield $y$ (timber volume in $\mbox{ft}^3$) of that stand is described by a "yield equation" $y=Y(t).$
Suppose that for a particular stand, the yield per tree is modeled by $$Y(t)=\frac{630t^2}{3t^2+8800}.$$
Application: Timber Yield
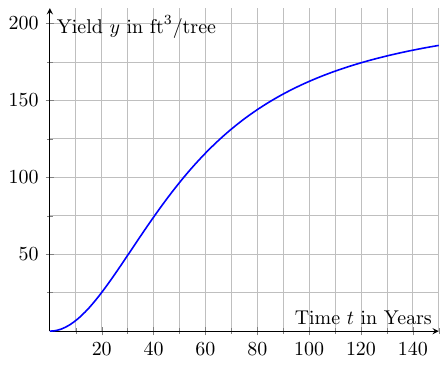 |
| $\displaystyle Y(t)=\frac{630t^2}{3t^2+8800}$ |
Find the rate at which the yield $Y$ is changing at $t=40$ years. What are the units of this value?
To find the rate at which the yield is changing at $t=40$ years, we find $Y'(40).$ But first,
$$
\begin{array}{lll}
Y'(t)&=\displaystyle \frac{d}{dt}\frac{630t^2}{3t^2+8800}&\\
&=\displaystyle \frac{(3t^2+8800)(630t^2)'-630t^2(3t^2+8800)'}{(3t^2+8800)^2}&\\
&=\displaystyle \frac{(3t^2+8800)(1260t)-630t^2\cdot 6t}{(3t^2+8800)^2}&\\
&=\displaystyle \frac{3780t^3+11088000t-3780t^3}{(3t^2+8800)^2}&\\
&=\displaystyle \frac{11088000t}{(3t^2+8800)^2}&\\
\end{array}
$$
Thus,
$$
\begin{array}{lll}
Y'(40)&=\displaystyle \frac{11088000\cdot 40}{(3(40)^2+8800)^2}&\\
&\approx 2.71
\end{array}
$$
That is, after $40$ years, the yield will be increasing by $2.71$ cubic feet per tree per year.
Application: The graph below gives data for the average rent for a two-bedroom domicile in San Francisco since January $2011.$
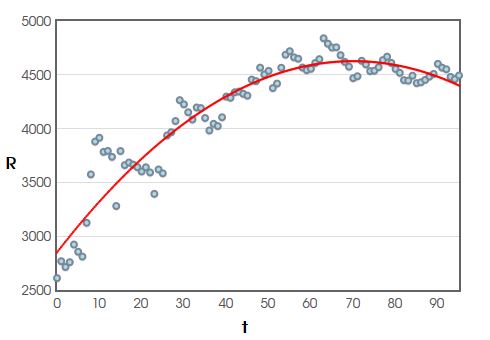
Estimate the rate of increase in rent at $t=30$ months. What are the units of this value?
To estimate the rate of increase in rent after $t=30$ months, we find $R'(30).$
First, we find $R'(t):$
$$
\begin{array}{lll}
R'(t)&=\displaystyle \frac{d}{dt} \left(-0.3625t^2+50.7599t+2850.3062\right)&\\
&\displaystyle =-0.3625\cdot 2t+50.7599\cdot 1+0&\\
&\displaystyle =-0.725t+50.7599&\\
\end{array}
$$
Thus, $R'(30)=-0.725\cdot 30+50.7599\approx 29.01.$
That is, at month $30,$ the average rent was increasing by about $\$29.01$ per month.
That is, at month $30,$ the average rent was increasing by about $\$29.01$ per month.