As we saw from the beginning of the last chapter, finding slopes of tangent lines is one of the big problems calculus seeks to solve.
Today, we will make the idea of "the slope of a tangent line" more precise.
The slope of the tangent line to a curve has a special name: the derivative.
The Derivative as Limit
| $y$ | | |
| $x$ |
Colorful Definition: Let $f(x)$ be a function defined in an open interval containing $a.$ The derivative of the function $f(x)$ at $a,$ denoted by $f'(a),$ is defined to be the limit
$f'(a)$ $\displaystyle =\lim_{h \rightarrow 0}$ $\displaystyle \frac{f(a+h)-f(a)}{h}$
provided this limit exists.
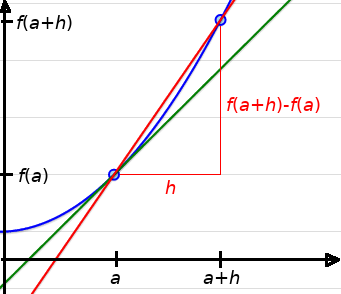
Austere, Textbook Definition: Let $f(x)$ be a function defined in an open interval containing $a.$ The derivative of the function $f(x)$ at $a,$ denoted by $f'(a),$ is defined to be the limit $$f'(a)=\lim_{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}$$ provided this limit exists.
Example: Using the Definition to Estimate a Derivative
For $f(x)=x^2$ at $x=a=1,$ the table below estimates $f'(1)$ for smaller and smaller values of $h.$
| $h$ | $\displaystyle \frac{f(1+h)-f(1)}{h}$ |
Example: Using the Definition to Find the Exact Value Derivative
For $f(x)=x^2,$ compute $f'(1).$
$$
\begin{array}{ll}
f'(1)&\\
=\displaystyle \lim_{h \rightarrow 0} \frac{f(1+h)-f(1)}{h}&\mbox{definition of the derivative}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{(1+h)^2-1}{h}&\mbox{since $f(x)=x^2$}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{1+2h+h^2-1}{h}&\mbox{after expanding square}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{2h+h^2}{h}&\mbox{after combining like terms}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{h(2+h)}{h}&\mbox{after factoring out $h$}\\
=\displaystyle \lim_{h \rightarrow 0} (2+h)&\mbox{after cancelling out $h$}\\
= 2& \mbox{using limit results}\\
\end{array}
$$
Example: Using the Definition to Find the Exact Value Derivative
For $\displaystyle f(x)=\frac{3}{x^2},$ compute $f'(3).$
$$
\begin{array}{ll}
f'(3)&\\
=\displaystyle \lim_{h \rightarrow 0} \frac{f(3+h)-f(3)}{h}&\mbox{definition of the derivative}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle \frac{3}{(3+h)^2}-\frac{3}{3^2}}{h}&\mbox{since $f(x)=\frac{3}{x^2}$}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle \frac{3}{(3+h)^2}-\frac{1}{3}}{h}&\mbox{after simplifying}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle \frac{3}{(3+h)^2}-\frac{1}{3}}{h}\frac{3(3+h)^2}{3(3+h)^2}&\mbox{multiply by a fancy 1 to cancel denominators}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle \left(\frac{3}{(3+h)^2}-\frac{1}{3}\right)3(3+h)^2}{h\cdot 3(3+h)^2}&\mbox{after multiplying}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle \frac{3}{(3+h)^2}\cdot 3(3+h)^2-\frac{1}{3}\cdot 3(3+h)^2}{3h(3+h)^2}&\mbox{after distributing}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle 9-(3+h)^2}{3h(3+h)^2}&\mbox{after cancelling denominators}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle 9-(9+6h+h^2)}{3h(3+h)^2}&\mbox{after expanding square}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle 9-9-6h-h^2}{3h(3+h)^2}&\mbox{after distributing the minus}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle -6h-h^2}{3h(3+h)^2}&\mbox{combine like terms}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle -h(6+h)}{3h(3+h)^2}&\mbox{after factoring out $-h$}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle -(6+h)}{3(3+h)^2}&\mbox{after cancelling $h$}\\
=\displaystyle \frac{-6}{27}&\mbox{using limit results}\\
=\displaystyle -\frac{2}{9}&\mbox{}\\
\end{array}
$$
Tangent Lines
As we saw in a previous section, the line tangent to a function at a point $(a,f(a))$ is, roughly speaking, the line which intersects the graph only at the point $(a,f(a)).$
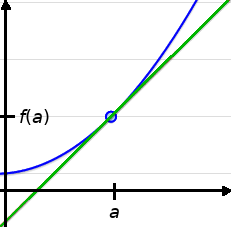
Tangent Lines
Recall: The point-slope form of a line is $y-y_0=m(x-x_0)$ where $m$ is the slope of the line and $(x_0,y_0)$ is a particular point on the line.
Since for the green line above $m=f'(a),$ and $(x_0,y_0)=(a,f(a)),$ we get the following "calculus" version of the point-slope form...
Tangent Lines
The tangent line of a function $f(x)$ at $x=a$ is given by $$y-f(a)=f'(a)(x-a)$$
Rearranging, we may write the above in slope-intercept form: $y=f'(a)x-af'(a)+f(a)$
Example: Tangent Lines
For $\displaystyle f(x)=\frac{3}{x^2},$ find the tangent line at $x=3.$
We begin with the general equation for the tangent line:
$$y-f(a)=f'(a)(x-a)$$
Since we are interested in the tangent line at $x=3,$ we have
$$y-f(3)=f'(3)(x-3).$$
Thus, to find the tangent line, all we need to do is find $f(3)$ and $f'(3).$
Now, $f(3)=\frac{3}{3^2}=\frac{1}{3},$ and $f'(3)=\frac{-2}{9}$ by the previous example. Thus, the equation of the tangent line can be expressed as $$y-\frac{1}{3}=-\frac{2}{9}(x-3).$$ Rearranging into slope intercept form we have $$y=-\frac{2}{9}x+1.$$
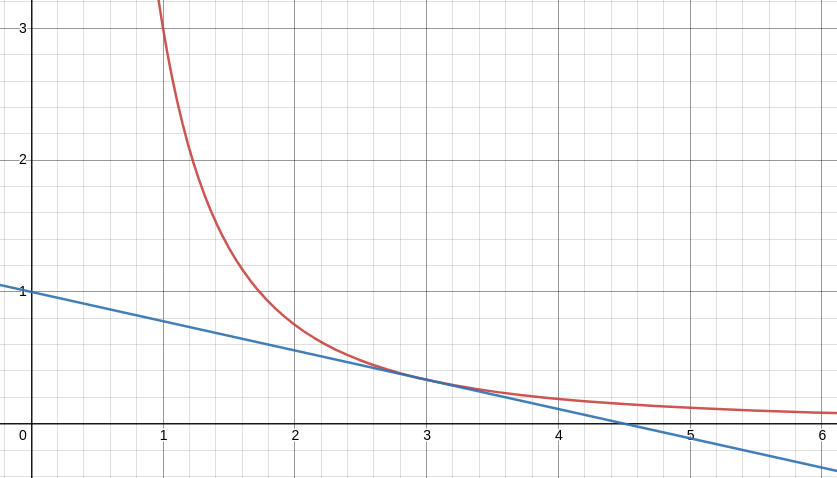
Now, $f(3)=\frac{3}{3^2}=\frac{1}{3},$ and $f'(3)=\frac{-2}{9}$ by the previous example. Thus, the equation of the tangent line can be expressed as $$y-\frac{1}{3}=-\frac{2}{9}(x-3).$$ Rearranging into slope intercept form we have $$y=-\frac{2}{9}x+1.$$
The Derivative as a Rate of Change
Recall: To interpret a slope (i.e., a derivative!), remember $$\mbox{units of derivative}=\mbox{units of slope}=\frac{\mbox{vertical units}}{\mbox{horizontal units}}$$
Average Rate of Change of a Function
The average rate of change of $f(x)$ over the interval $[a,a+h]$ is $\displaystyle \frac{f(a+h)-f(a)}{h}.$
Instantaneous Rate of Change
The instantaneous rate of change of $f(x)$ at $x=a,$ is $\displaystyle f'(a).$
This is because $f'(a)$ is the limiting value of the difference quotient $\displaystyle \frac{f(a+h)-f(a)}{h}$ as $h$ approaches $0.$
Rate of Change Example: Velocity
Velocity is the rate at which an object's position changes with respect to time.
Suppose we have a function which gives an object's distance in meters with respect to time in seconds, say $s(t).$
What is the meaning of $s'(t)?$
Hint: What are its units?
Example: Velocity
The graph gives the distance an automobile has travelled after different periods of time. Determine the slope of this line, and then interpret the meaning of this rate of change.
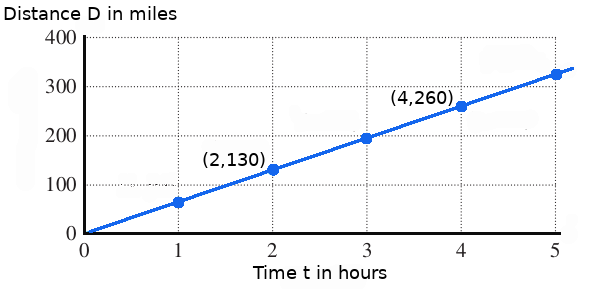
Remember, the interpretation of slope is $\frac{\mbox{vertical units}}{\mbox{horizontal units}}$.
Example: Velocity
Using propane, ethanol, methanol and butane, a potato cannon produce muzzle velocities of between $28$ and $48$ meters per second. (Source: U.S. Air Force Measures Potato Cannon Muzzle Velocities).
Suppose the muzzle velocity of a potato cannon is $32$ m/s and that the downward acceleration due to gravity is $9.8$ m/s2. Then, when fired vertically, the height $s$ in meters of the potato above the ground $t$ seconds after firing can be expressed (ignoring air resistance) as $s(t)=-4.9t^2+32t.$
What is the velocity of the potato $2$ seconds after firing?
$$
\begin{array}{ll}
s'(2)&\\
=\displaystyle \lim_{h \rightarrow 0} \frac{s(2+h)-s(2)}{h}&\mbox{definition of the derivative}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{-4.9(2+h)^2+32(2+h)-(-4.9\cdot 2^2 +32 \cdot 2)}{h}&\mbox{since $s(t)=-4.9t^2+32t$}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{-4.9(4+4h+h^2)+32(2+h)+4.9\cdot 2^2 -32 \cdot 2}{h}&\mbox{expand square and distribute minus}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{-4.9\cdot 4-4.9\cdot 4h-4.9\cdot h^2+32\cdot 2+ 32h+4.9\cdot 2^2 -32 \cdot 2}{h}&\mbox{distribute $-4.9$}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{-4.9\cdot 4h-4.9\cdot h^2+ 32h}{h}&\mbox{cancel lots of stuff}\\
=\displaystyle \lim_{h \rightarrow 0} \frac{12.4h-4.9\cdot h^2}{h}&\mbox{simplify}\\
=\displaystyle \lim_{h \rightarrow 0} (12.4-4.9h)&\mbox{after cancelling $h$}\\
=12.4&\mbox{using limit results}\\
\end{array}
$$
Average Versus Instantaneous Velocity
Consider the equation $s(t)=-4.9t^2+32t$ of the height of our potato with respect to time. The instantaneous velocity of the potato at $t=2$ seconds is $s'(2)=12.4$ m/s
Example: The graph below gives data for the average rent for a two bedroom domicile in San Francisco since January 2011.
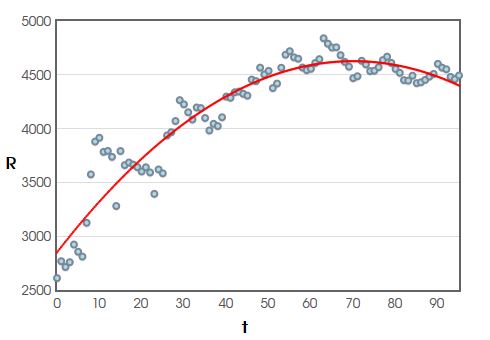
Use this curve $R(t)$ to estimate the average rate of increase in rent from month $30$ to month $50$ and interpret the result.
The change in $t$ from $t=30$ to $t=50$ is $h=50-30=20.$
Then the average rate of increase in rent from month $30$ to month $50$ is given by
$$
\begin{array}{l}
\displaystyle \frac{R(30+h)-R(30)}{h}\\
\displaystyle=\frac{R(50)-R(30)}{20}\\
\displaystyle=\frac{-0.3625({\bf 50})^2+50.7599\cdot {\bf 50}+2850.3062-(-0.3625({\bf 30})^2+50.7599\cdot {\bf 30}+2850.3062)}{20}\\
\displaystyle=\frac{435.198}{20}\\
=21.7599\\
\approx 21.76\\
\end{array}
$$
The average rate of increase of rent from month $30$ to month $50$ was about $\$21.76$ per month.