The Precise Definition of a Limit

The Precise Definition of a Limit

Today we make the notion of limit precise.

The ideas we will be discussing today are the foundation upon which calculus rests (as well as other areas of advanced mathematics).

Recall: The Intuitive Definition of a Limit

Let $f(x)$ be a function defined at all values in an open interval containing $a,$ with the possible exception of $a$ itself, and let $L$ be a real number.

Then $$\displaystyle \lim_{x \rightarrow a} f(x)=L$$ if all values of the function $f(x)$ approach the real number $L$ as the values of $x$ (not equal to $a$) approach the number $a.$

The Precise Definition of a Limit

Let $f(x)$ be defined for all $x \neq a$ over an open interval containing $a.$ Let $L$ be a real number.

Then $$\displaystyle \lim_{x \rightarrow a} f(x)=L$$ means that for every $\varepsilon \gt 0$ there exists a $\delta\gt 0$ such that $0 \lt |x-a| \lt \delta \implies |f(x)-L| \lt \varepsilon.$

Remark

For every $\varepsilon \gt 0$ there exists a $\delta\gt 0$ such that $0 \lt |x-a| \lt \delta \implies |f(x)-L| \lt \varepsilon.$

A way to interpret the above statement is:

"We can make $f(x)$ as close to $L$ as we like by making $x$ sufficiently close to $a.$"

The $\varepsilon$-$\delta$ Definition of a Limit (Limit Exists)

$\displaystyle \lim_{x \rightarrow a} f(x)=L$ means:

for any $\varepsilon \gt 0$ we choose,
we can find a $\delta \gt 0$ such that
$0 \lt |x-a| \lt \delta$ (any $x$-value in pink strip)
guarantees that $|f(x)-L| \lt \varepsilon$
($f(x)$-value in blue strip)

Example

Consider the limit $\displaystyle \lim_{x \rightarrow 2} (3x-2)=4.$

Suppose $\varepsilon = 0.3.$ Find a $\delta \gt 0$ so that $$0 \lt |x-2|\lt \delta \implies |f(x)-L|=|(3x-2)-4| \lt \varepsilon=0.3.$$

$$ \begin{array}{ll} |f(x)-L|=|(3x-2)-4|<\varepsilon=0.3 &\\ |3x-6| \lt 0.3&\\ |3(x-2)| \lt 0.3&\\ |3||x-2| \lt 0.3& \mbox{An absolute value of a product is the product of the absolute values.}\\ 3|x-2| \lt 0.3&\\ |x-2| \lt 0.1.&\\ \end{array} $$ Thus, taking $\delta=0.1$ will suffice. In fact, any $\delta$ less than $0.1$ will do the trick.

Taking it to the Limit

To prove the limit requires that we show that we can find a $\delta \gt 0$ that works any $\varepsilon \gt 0.$

Example

Use the precise definition of a limit to show that $\displaystyle \lim_{x \rightarrow 2} (3x-2)=4.$

Prep-Work: Find the $\delta$ which will work for any $\varepsilon \gt 0:$ $$ \begin{array}{ll} |f(x)-L|=|(3x-2)-4|<\varepsilon &\\ |3x-6| \lt \varepsilon&\\ |3(x-2)| \lt \varepsilon&\\ |3||x-2| \lt \varepsilon& \mbox{An absolute value of a product is the product of the absolute values.}\\ 3|x-2| \lt \varepsilon&\\ |x-2| \lt \frac{\varepsilon}{3}.&\\ \end{array} $$ Thus, taking $\displaystyle \delta=\frac{\varepsilon}{3}$ will suffice.

With our $\delta$ in hand, we may now formally prove the limit: $$\displaystyle \lim_{x \rightarrow 2} (3x-2)=4.$$ Proof: Let $\varepsilon \gt 0.$ Choose $\delta=\frac{\varepsilon}{3}.$ Then, $$ \begin{array}{ll} 0\lt |x-2| \lt \delta&\\ \implies |x-2| \lt \frac{\varepsilon}{3}&\\ \implies 3|x-2| \lt \varepsilon&\\ \implies|3||x-2| \lt \varepsilon& \mbox{An absolute value of a product is the product of the absolute values.}\\ \implies|3(x-2)| \lt \varepsilon&\\ \implies|3x-6| \lt \varepsilon&\\ \implies|(3x-2)-4|\lt \varepsilon &\\ \implies|f(x)-L| \lt \varepsilon&\\ \end{array} $$ $\square$

Strategy for Proving a Limit

1. Begin the proof with the following statement: "Let $\varepsilon \gt 0.$"

2. Next, we need to obtain a value for $\delta.$ After we have obtained this value, we make the following statement, filling in the blank with our choice of $\delta:$ "Choose $\delta=$_______." (This is generally a statement involving $\varepsilon.$)

3.The next statement in the proof should be: "Assume $0 \lt |x−a| \lt \delta.$" (At this point, we fill in our given value for $a$).

4. Next, based on this assumption, we need to show that $0 <|x−a|<\delta \implies |f(x)−L| \lt \varepsilon,$ where $f(x)$ and $L$ are our function $f(x)$ and our limit $L.$ Generally this will involve several steps: $0 <|x−a|<\delta \implies \mbox{Statement 1} \implies \mbox{Statement 2} \implies \cdots \implies |f(x)−L| \lt \varepsilon$

5. (Optional Gloat Line) We conclude our proof with the statement: "Therefore, $\displaystyle \lim_{x \rightarrow a} f(x)=L.$"

Sometimes finding the right $\delta$ can be trickier...

Example

Use the precise definition of a limit to show that $\displaystyle \lim_{x \rightarrow 9} \sqrt{x}=3.$

Prep-Work: Find the $\delta$ which will work for any $\varepsilon \gt 0:$ $$ \begin{array}{ll} |f(x)-L| \lt \varepsilon &\\ |\sqrt{x}-3| \lt \varepsilon &\\ -\varepsilon \lt \sqrt{x}-3 \lt \varepsilon &\\ -\varepsilon+3 \lt \sqrt{x} \lt \varepsilon+3 &\\ (-\varepsilon+3)^2 \lt x \lt (\varepsilon+3)^2 &\\ \varepsilon^2-6\varepsilon +9\lt x \lt \varepsilon^2+6\varepsilon +9 &\\ \varepsilon^2-6\varepsilon\lt x-9 \lt \varepsilon^2+6\varepsilon &\\ \end{array} $$ At this point, it's not entirely clear what we should take as $\delta.$ A picture of the situation will help us here.

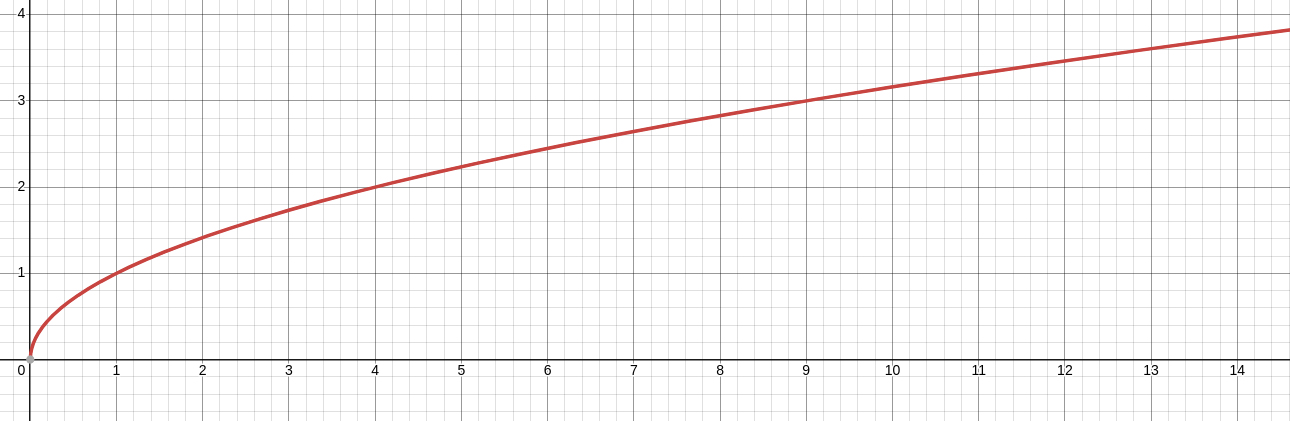
From the picture, we need to take the the endpoint of the interval which is shorter. That is, we take the left-hand endpoint: $-\delta=\varepsilon^2-6\varepsilon.$ Thus, $\delta=6\varepsilon-\varepsilon^2.$ This is the $\delta$ that will make the proof work.

With our $\delta$ in hand, we may now formally prove the limit: $$\displaystyle \lim_{x \rightarrow 9} \sqrt{x}=3.$$ Proof: Let $\varepsilon \gt 0.$ Choose $\delta=6\varepsilon-\varepsilon^2.$ Then, $$ \begin{array}{ll} 0 \lt |x-9| \lt \delta&\\ \implies |x-9| \lt 6\varepsilon-\varepsilon^2&\\ \implies -(6\varepsilon-\varepsilon^2) \lt x-9 \lt 6\varepsilon-\varepsilon^2&\\ \implies -6\varepsilon+\varepsilon^2 \lt x-9 \lt 6\varepsilon-\varepsilon^2&\\ \implies \varepsilon^2-6\varepsilon \lt x-9 \lt 6\varepsilon-\varepsilon^2&\\ \implies \varepsilon^2-6\varepsilon \lt x-9 \lt 6\varepsilon+\varepsilon^2& \mbox{since $6\varepsilon-\varepsilon^2 \lt 6\varepsilon+\varepsilon^2$}\\ \implies \varepsilon^2-6\varepsilon +9 \lt x \lt \varepsilon^2+6\varepsilon+9&\\ \implies \varepsilon^2-6\varepsilon +9 \lt x \lt \varepsilon^2+6\varepsilon+9&\\ \implies (-\varepsilon+3)^2 \lt x \lt (\varepsilon+3)^2&\\ \implies -\varepsilon+3 \lt \sqrt{x} \lt \varepsilon+3&\\ \implies -\varepsilon \lt \sqrt{x}-3 \lt \varepsilon&\\ \implies |\sqrt{x}-3| \lt \varepsilon&\\ \end{array} $$ $\square$

Example

Use the precise definition of a limit to show that $\displaystyle \lim_{x \rightarrow 1} x^2=1.$

Prep-Work: Find the $\delta$ which will work for any $\varepsilon \gt 0:$ $$ \begin{array}{ll} |f(x)-L| \lt \varepsilon &\\ |x^2-1| \lt \varepsilon &\\ |(x+1)(x-1)| \lt \varepsilon &\\ |x+1||x-1| \lt \varepsilon & \mbox{An absolute value of a product is the product of the absolute values.}\\ \end{array} $$ Again, it's not entirely clear what $\delta$ should be. The problem is that pesky $|x+1|$ factor in the above expression.

It may seem like a burst of divine inspiration, but here's a common trick: take $\delta=1$ and see if there's a bound on the $|x+1|$ factor.

We know that $|x-1|\lt \delta=1$ implies that $-1 \lt x-1 \lt 1.$

Adding $2$ to all sides gives $1 \lt x+1 \lt 3.$

Then it is also true that $-3 \lt x+1 \lt 3$ which gives $|x+1| \lt 3.$

Thus, the $|x+1|$ factor is bounded by $3$ as long as we choose our $\delta \leq 1.$

With this we can continue from where we left off!

If $\delta \leq 1,$ then $|x+1||x-1| \lt \varepsilon$ implies that $$3|x-1| \lt \varepsilon.$$ Then $|x-1| \lt \frac{\varepsilon}{3}.$ Thus, it must also be that $\delta \leq \frac{\varepsilon}{3}.$

We now have everything we need: as long a $\delta \leq 1$ AND $\delta \leq \frac{\varepsilon}{3},$ we get what we want.

To make sure both conditions are satisfied we take $\delta=\min\{1,\frac{\varepsilon}{3}\}.$ This is our delta! :D

With our $\delta$ in hand, we may now formally prove the limit: $$\displaystyle \lim_{x \rightarrow 1} x^2=1.$$ Proof: Let $\varepsilon \gt 0.$ Choose $\delta=\min\{1,\frac{\varepsilon}{3}\}.$ Then, $|x-1| \lt \delta$ implies that $|x-1|\lt 1$ which implies that $|x+1|\lt 3.$ But $|x-1| \lt \delta$ also implies that $|x-1| \lt \frac{\varepsilon}{3}.$ Therefore, $$ \begin{array}{ll} 0 \lt |x-1| \lt \delta&\\ \implies |x-1| \lt \min\{1,\frac{\varepsilon}{3}\}&\\ \implies |x+1| \lt 3 \mbox{ AND } |x-1| \lt \frac{\varepsilon}{3}&\\ \implies |x+1||x-1| \lt 3\cdot \frac{\varepsilon}{3}&\\ \implies |(x+1)(x-1)| \lt \varepsilon& \mbox{An absolute value of a product is the product of the absolute values.}\\ \implies |x^2-1| \lt \varepsilon.& \mbox{}\\ \end{array} $$ $\square$

Example: Limit Laws

Prove the following limit law:

Let $f(x)$ be defined for all $x \neq a$ over some open interval containing $a.$ Assume that $L$ is a real number such that $\displaystyle \lim_{x \rightarrow a} f(x)=L.$

Then $\displaystyle \lim_{x \rightarrow a}cf(x)=c\lim_{x \rightarrow a} f(x)=cL$ for any constant $c.$

Prep-Work: Find the $\delta$ which will work for any $\varepsilon \gt 0:$ $$ \begin{array}{ll} |cf(x)-cL|<\varepsilon &\\ |c(f(x)-L)|<\varepsilon &\\ |c||f(x)-L| \lt \varepsilon& \mbox{An absolute value of a product is the product of the absolute values.}\\ |f(x)-L| \lt \frac{\varepsilon}{|c|}& \\ \end{array} $$ The above will act as a guide. However, in this situation, since we have that $\displaystyle \lim_{x \rightarrow a} f(x)=L$ exists, we don't actually need to explicitly find $\delta;$ it's guaranteed by the existence of the limit. With the above in mind, we now formally prove the limit law:

Let $f(x)$ be defined for all $x \neq a$ over some open interval containing $a.$ Assume that $L$ is a real number such that $\displaystyle \lim_{x \rightarrow a} f(x)=L.$

Then $\displaystyle \lim_{x \rightarrow a}cf(x)=c\lim_{x \rightarrow a} f(x)=cL$ for any constant $c.$

Proof: Let $\varepsilon \gt 0.$ Since $\displaystyle \lim_{x \rightarrow a} f(x)=L$ exists, we may may find a $\delta \gt 0$ such that $$ |x-a| \lt \delta \implies |f(x)-L| \lt \frac{\varepsilon}{|c|}. $$ Then, $$ \begin{array}{ll} |x-a| \lt \delta&\\ \implies |f(x)-L| \lt \frac{\varepsilon}{|c|}&\\ \implies |c||f(x)-L| \lt \varepsilon&\\ \implies |c(f(x)-L)| \lt \varepsilon&\mbox{An absolute value of a product is the product of the absolute values.}\\ \implies |cf(x)-cL| \lt \varepsilon&\\ \end{array} $$ $\square$

Story Time

If the precise definition of a limit is making your head spin, take comfort in the fact that it took the greatest minds in mathematics about $200$ years to formulate it.

Newton	Leibniz	Cauchy	Weirstrass

1643-1727	1646-1716	1789-1857	1815-1897

Showing a Limit Doesn't Exist

The $\varepsilon$-$\delta$ Definition of a Limit (Limit Does Not Exist)

$\displaystyle \lim_{x \rightarrow a} f(x)$ does not exist means:

There is an $\varepsilon \gt 0$,
such that for any $\delta \gt 0$ and any real number $L$, there
is an $x$ such that $0 \lt |x-a| \lt\delta$
(for some $x$-value in pink strip)
that gives $|f(x)-L| \geq \varepsilon$
($f(x)$-value NOT in blue strip)

Example

Use the definition of a limit to show that the limit $$\displaystyle \lim_{x \rightarrow 2} \frac{|x^2-4|}{x-2}$$ does not exist.

Proof: Choose $\varepsilon =1.$ We must show that for any $\delta \gt 0$ and any number $L,$ we can find an $x$ in the interval given by $0 \lt |x-2| \lt \delta$ such that $$|f(x)-L|=\left|\displaystyle \frac{|x^2-4|}{x-2}-L\right| \geq 1=\varepsilon.$$ Case 1: Suppose $L \geq 1.$ Choose $x=2-\frac{\delta}{2}.$ We note that $x$ satisfies $0 \lt |x-2| \lt \delta.$ Then, $$ \begin{array}{ll} |f(x)-L|&\\ =\left|\displaystyle \frac{|x^2-4|}{x-2}-L\right|&\\ =\left|\displaystyle \frac{|(x-2)(x+2)|}{x-2}-L\right|&\\ =\left|\displaystyle \frac{|x-2||x+2|}{x-2}-L\right|& \mbox{The absolute value of a product is the product of the absolute values.}\\ =\left|\displaystyle \frac{|2-\frac{\delta}{2}-2||2-\frac{\delta}{2}+2|}{2-\frac{\delta}{2}-2}-L\right|& \mbox{since we chose $x=2-\frac{\delta}{2}$}\\ =\left|\displaystyle \frac{|-\frac{\delta}{2}||4-\frac{\delta}{2}|}{-\frac{\delta}{2}}-L\right|& \mbox{}\\ =\left|\displaystyle -\left|4-\frac{\delta}{2}\right|-L\right| & \mbox{$\frac{|-\frac{\delta}{2}|}{-\frac{\delta}{2}}=-1$ since $\delta \gt 0$}\\ =\left|\displaystyle -\left(\left|4-\frac{\delta}{2}\right|+L\right)\right| & \mbox{ }\\ =\left|\displaystyle \left|4-\frac{\delta}{2}\right|+L\right| & \mbox{since $|-\mbox{stuff}|=|\mbox{stuff}|$}\\ \geq |L|&\\ =L&\mbox{since $L \geq 1$} &\\ \geq 1& \\ =\varepsilon &\\ \end{array} $$ Case 2: Suppose $L \lt 1.$ Choose $x=2+\frac{\delta}{2}.$ We note here also that $x$ satisfies $0 \lt |x-2| \lt \delta.$ Then, $$ \begin{array}{ll} |f(x)-L|&\\ =\left|\displaystyle \frac{|x^2-4|}{x-2}-L\right|&\\ =\left|\displaystyle \frac{|(x-2)(x+2)|}{x-2}-L\right|&\\ =\left|\displaystyle \frac{|x-2||x+2|}{x-2}-L\right|& \mbox{The absolute value of a product is the product of the absolute values.}\\ =\left|\displaystyle \frac{|2+\frac{\delta}{2}-2||2+\frac{\delta}{2}+2|}{2+\frac{\delta}{2}-2}-L\right|& \mbox{since we chose $x=2-\frac{\delta}{2}$}\\ =\left|\displaystyle \frac{|\frac{\delta}{2}||4+\frac{\delta}{2}|}{\frac{\delta}{2}}-L\right|& \mbox{}\\ =\left|\displaystyle \left|4+\frac{\delta}{2}\right|-L\right| & \mbox{$\frac{|\frac{\delta}{2}|}{\frac{\delta}{2}}=1$ since $\delta \gt 0$}\\ =\left|\displaystyle 4+\frac{\delta}{2}-L\right| & \mbox{since $\delta \gt 0$}\\ \gt \left|\displaystyle 4+\frac{\delta}{2}-1\right|&\mbox{since $L \lt 1$}\\ =\left|\displaystyle 3+\frac{\delta}{2}\right|&\mbox{}\\ =\displaystyle 3+\frac{\delta}{2}&\mbox{since $\delta \gt 0$}\\ \geq 1&\\ =\varepsilon &\\ \end{array} $$ $\square$

One-Sided Limits

Left-Hand Limit: Let $f(x)$ be defined for all $x$ on an open interval $(c,a)$ Then $$\displaystyle \lim_{x \rightarrow a^-} f(x)=L$$ means that for every $\varepsilon \gt 0$ there exists a $\delta\gt 0$ such that $0 \lt a-x \lt \delta \implies |f(x)-L| \lt \varepsilon.$

Right-Hand Limit: Let $f(x)$ be defined for all $x$ on an open interval $(a,b)$ Then $$\displaystyle \lim_{x \rightarrow a^+} f(x)=L$$ means that for every $\varepsilon \gt 0$ there exists a $\delta\gt 0$ such that $0 \lt x-a \lt \delta \implies |f(x)-L| \lt \varepsilon.$

One-Sided Limits

Example: Use the definition of a left-hand limit to show that $$\displaystyle \lim_{x \rightarrow 2^-} \frac{|x^2-4|}{x-2}=-4$$

Prep-Work: Let $0 \lt 2-x \lt \delta.$ In other words, let $2-\delta \lt x \lt 2.$ This is to say that $x$ is "just to the left" of $2.$ Then $$\displaystyle \frac{|x^2-4|}{x-2}=\frac{|(x-2)(x+2)|}{x-2}=\frac{|x-2||x+2|}{x-2}.$$ Since we are assuming $x$ is to the left of $2,$ we can say that $x-2$ is negative. Then, $\frac{|x-2|}{x-2}=-1$ so that $$\displaystyle \frac{|x^2-4|}{x-2}=-|x+2|.$$ Furthermore, if $x \gt -2,$ then $-|x+2|=-(x+2).$ We can then say that $\displaystyle \lim_{x \rightarrow 2^-} \frac{|x^2-4|}{x-2}=\displaystyle \lim_{x \rightarrow 2^-}[-(x+2)]=-\displaystyle \lim_{x \rightarrow 2^-}(x+2).$ Thus, to prove the original limit, all we need to prove is that $$\displaystyle \lim_{x \rightarrow 2^-}(x+2)=4.$$ We can now decide on which $\delta$ to choose: $$ \begin{array}{ll} |(x+2)-4|\lt \varepsilon &\\ |x-2| \lt \varepsilon &\\ -\varepsilon \lt x-2 \lt \varepsilon &\\ 2-x \lt \varepsilon &\\ \end{array} $$ The above hints that choosing $\delta=\varepsilon$ will work just fine! ;) We now have everything we need to prove our limit:

$$\displaystyle \lim_{x \rightarrow 2^-} \frac{|x^2-4|}{x-2}=-4$$

Proof: Let $\varepsilon \gt 0.$ Choose $\delta = \varepsilon.$ Then, $$ \begin{array}{ll} 0 \lt 2-x \lt \delta&\\ \implies 0 \lt 2-x \lt \varepsilon& \mbox{since we chose $\delta=\epsilon$}\\ \implies -\varepsilon \lt x-2 \lt 0&\\ \implies -\varepsilon \lt x-2 \lt \varepsilon &\\ \implies |x-2| \lt \varepsilon&\\ \implies |(x+2)-4| \lt \varepsilon &\\ \end{array} $$ Thus, we have shown that $$\displaystyle \lim_{x \rightarrow 2^-}(x+2)=4.$$ We then have $$ \begin{array}{ll} \displaystyle\lim_{x \rightarrow 2^-} \frac{|x^2-4|}{x-2}&\\ =\displaystyle\lim_{x \rightarrow 2^-} \frac{-(x^2-4)}{x-2}& \mbox{since $0 \lt 2-x \lt \delta$ ($x$ is just the left of $2$)}\\ =\displaystyle\lim_{x \rightarrow 2^-} [-(x+2)]& \mbox{after simplifying and noting that $x$ is never actually equal to 2}\\ =-\displaystyle\lim_{x \rightarrow 2^-} (x+2)& \mbox{A limit of a multiple is a multiple of the limits.}\\ =-4& \mbox{as shown above}\\ \end{array} $$ $\square$

Let's Recall a Useful Theorem

Recall that two-sided limits and one-sided limits are related. Intuitively, it makes sense that if the left and right-hand limits exist, and both are the same value $L,$ then the two sided limit exists. Conversely, if the two-sided limit exists and is equal to $L,$ then the left and right-hand limits also exist and are equal to $L.$

Theorem

Let $f(x)$ be a function defined at all values in an open interval containing $a,$ with the possible exception of $a$ itself, and let $L$ be a real number. Then,

$\displaystyle \lim_{x \rightarrow a} f(x)=L$ if and only if $\displaystyle \lim_{x \rightarrow a^{+}} f(x)=L$ and $\displaystyle \lim_{x \rightarrow a^{-}} f(x)=L.$

Proof:

Suppose $\displaystyle \lim_{x \rightarrow a} f(x)=L$ and let $\varepsilon \gt 0.$ Choose $\delta \gt 0$ such that $0 \lt |x-a| \lt \delta \implies |f(x)-L| \lt \varepsilon.$ Then, $$ \begin{array}{ll} 0 \lt x-a \lt \delta &\\ \implies 0 \lt |x-a| \lt \delta&\\ \implies |f(x)-L| \lt \varepsilon.& \end{array} $$ Thus, $\displaystyle \lim_{x \rightarrow a^{+}} f(x)=L.$

Similarly, $$ \begin{array}{ll} 0 \lt a-x \lt \delta&\\ \implies -\delta \lt x-a \lt 0&\\ \implies 0 \lt |x-a| \lt \delta\\ \implies |f(x)-L| \lt \varepsilon.\\ \end{array} $$ Thus, $\displaystyle \lim_{x \rightarrow a^{-}} f(x)=L.$

For the converse, suppose that $\displaystyle \lim_{x \rightarrow a^{+}} f(x)=L$ and $\displaystyle \lim_{x \rightarrow a^{-}} f(x)=L.$ Let $\varepsilon \gt 0.$ By the our hypothesis, we know that for some $\delta_1 \gt 0$ $$ 0 \lt x-a \lt \delta_1 \implies |f(x)-L| \lt \varepsilon\\ $$ and for some $\delta_2 \gt 0$ $$ 0 \lt a-x \lt \delta_2 \implies |f(x)-L| \lt \varepsilon. $$ Choose $\delta=\min\{\delta_1,\delta_2\}.$ Then, by the above, $$ \begin{array}{ll} 0 \lt |x-a| \lt \delta\\ \implies -\delta_2 \leq -\delta \lt x-a \lt 0 \lt x-a \lt \delta \leq \delta_1&\\ \implies |f(x)-L| \lt \varepsilon.\\ \end{array} $$ Thus, $\displaystyle \lim_{x \rightarrow a} f(x)=L.$

$\square$

Some Remarks

Using the above theorem, it is much easier to prove that a limit does not exist: if the left and right-hand limits don't agree, then the limit doesn't exist.

We showed with relative ease above that $\displaystyle \lim_{x \rightarrow 2^{-}} \frac{|x^2-4|}{x-2}=-4.$

Showing rigorously that $\displaystyle \lim_{x \rightarrow 2^{+}} \frac{|x^2-4|}{x-2}=4$ is also relatively straightforward.

Thus, since the left and right hand limits don't agree, the two sided limit $\displaystyle \lim_{x \rightarrow 2} \frac{|x^2-4|}{x-2}$ doesn't exist.

Infinite Limits

Recall that for some functions $f$ we can make the value of $f(x)$ as large as we like (in either the positive or negative direction) by making $x$ sufficiently close to some value $a$. In this case we say that $$\displaystyle \lim_{x \rightarrow a} f(x)=\infty \,\,\,\, \mbox{ or } \,\,\,\, \lim_{x \rightarrow a} f(x)=-\infty$$ We now present the precise definition of this idea.

Definition

Limit at Positive Infinity Let $f(x)$ be defined for all $x \neq a$ in an open interval containing $a.$ Then, we have a positive infinite limit $$\lim_{x \rightarrow a} f(x)=\infty$$ if for every $M \gt 0$ there exists $\delta \gt 0$ such that $0 \lt |x−a| \lt \delta \implies f(x) \gt M.$

Limit at Negative Infinity Let $f(x)$ be defined for all $x \neq a$ in an open interval containing $a.$ Then, we have a negative infinite limit $$\lim_{x \rightarrow a} f(x)=-\infty$$ if for every $M \lt 0$ there exists $\delta \gt 0$ such that $0 \lt |x−a| \lt \delta \implies f(x) \lt M.$

Limit at Infinity $$\lim_{x \rightarrow a} f(x)=\infty$$ if for every $M \gt 0$ there exists $\delta \gt 0$ such that $0 \lt |x−a| \lt \delta \implies f(x) \gt M.$

Limit at Infinity

Use the definition of an infinite limit to show that $$\lim_{x \rightarrow 1} \frac{1}{(x-1)^2}=\infty.$$

Prep-Work: Find the $\delta$ which will to make $f(x)$ larger than an arbitrary $M \gt 0:$ $$ \begin{array}{ll} f(x)\gt M &\\ \displaystyle \frac{1}{(x-1)^2} \gt M &\\ (x-1)^2 \lt \displaystyle \frac{1}{M} &\\ |x-1| \lt \sqrt{\displaystyle\frac{1}{M}} & \mbox{since $\sqrt{\mbox{stuff}^2}=|\mbox{stuff}|$}\\ \end{array} $$ Thus, we take $\delta$ to be $\sqrt{\displaystyle\frac{1}{M}}.$

With our $\delta$ in hand, we may now formally prove the limit: $$\lim_{x \rightarrow 1} \frac{1}{(x-1)^2}=\infty.$$ Proof: Let $M \gt 0.$ Choose $\delta=\sqrt{\displaystyle\frac{1}{M}}.$ Then, $$ \begin{array}{ll} 0 \lt |x-1| \lt \sqrt{\displaystyle\frac{1}{M}} & \mbox{}\\ \implies (x-1)^2 \lt \displaystyle \frac{1}{M} &\\ \implies \displaystyle \frac{1}{(x-1)^2} \gt M &\\ \implies f(x)\gt M &\\ \end{array} $$ $\square$