What does it mean for a curve to be continuous? Does it mean that you should be able to trace along the curve without having to lift your pencil?
Today, we shall get closer to the heart of one of the deepest notions in mathematics: continuity.
Continuity: A Formal Definition
A function $f(x)$ is continuous at a point $a$ if and only if the following three conditions are satisfied:
i. $\,\,\,\,f(a)$ is defined
ii. $\,\,\,\, \displaystyle \lim_{x \rightarrow a} f(x)$ exists
iii. $\,\,\,\, \displaystyle \lim_{x \rightarrow a} f(x)=f(a)$
A function is discontinuous at a point $a$ if it fails to be continuous at $a.$
Example: The function $f$ below is continuous at $x=2$ because $\displaystyle \lim_{x \rightarrow 2} f(x)=f(2)=8.$
| $y$ | | |
| $x$ |
Example: The function $f$ below is NOT continuous at $x=2$ because $\displaystyle \lim_{x \rightarrow 2} f(x)=8 \neq f(2)=20.$
| $y$ | | |
| $x$ |
Example: The function $f$ below is NOT continuous at $x=2$ because $f(2)$ is undefined.
| $y$ | | |
| $x$ |
Example: The function $f$ below is NOT continuous at $x=2$ because $\displaystyle \lim_{x \rightarrow 2} f(x)$ does not exist.
| $y$ | | |
| $x$ |
Discontinuities
The following are ways a function $f$ can be discontinuous at a point $x=a.$
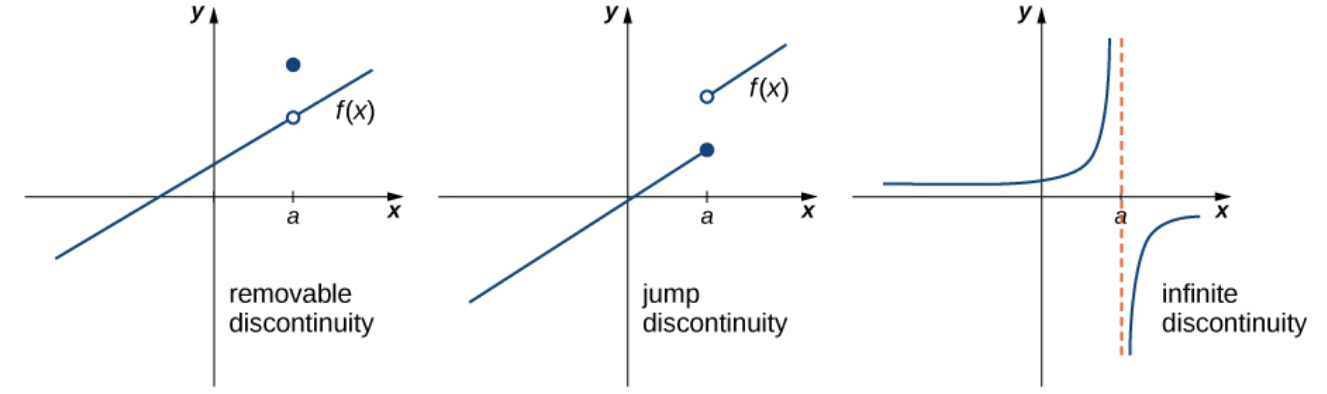
Example
Consider the function $$f(x)=\begin{cases}2x+1 & \mbox{ if $x \lt 1$} \\ 2 & \mbox{ if $x=1$} \\ -x+4 & \mbox{ if $x \gt 1$} \end{cases}$$ a. Using the definition of continuity, determine whether the function is continuous at $x=1.$
Observe that $\displaystyle \lim_{x \rightarrow 1^-}f(x)=3$ and $\displaystyle \lim_{x \rightarrow 1^+}f(x)=3.$
Thus, $\displaystyle \lim_{x \rightarrow 1}f(x)=3$.
Hence, $f(x)$ cannot be continuous at $x=1$ since $\displaystyle \lim_{x \rightarrow 1}f(x)=3 \neq 2 =f(1).$
Thus, $\displaystyle \lim_{x \rightarrow 1}f(x)=3$.
Hence, $f(x)$ cannot be continuous at $x=1$ since $\displaystyle \lim_{x \rightarrow 1}f(x)=3 \neq 2 =f(1).$
b. If it is discontinuous, what type of discontinuity is it?
It is a removable discontinuity.
Example
Consider the function $$ f(x)= \begin{cases} x+3, & x \lt 1 \\ (x-2)^2, & x \geq 1 \end{cases} $$ a. Using the definition of continuity, determine whether the function is continuous at $x=1.$
Observe that $\displaystyle \lim_{x \rightarrow 1^-}f(x)=4$ and $\displaystyle \lim_{x \rightarrow 1^+}f(x)=1.$
Thus, $\displaystyle \lim_{x \rightarrow 1}f(x)$ does not exist.
Hence, $f(x)$ cannot be continuous at $x=1.$
Thus, $\displaystyle \lim_{x \rightarrow 1}f(x)$ does not exist.
Hence, $f(x)$ cannot be continuous at $x=1.$
b. If it is discontinuous, what type of discontinuity is it?
JUMP!




Example
Consider the function $$f(t)=\frac{t+3}{t^2+5t+6}$$ a. Determine the point(s), if any, at which the function is discontinuous.
The function $f(t)$ is discontinuous at $t$ for which the denominator is $0.$
Thus, we solve $t^2+5t+6=0$ to find points of discontinuity: $$t^2+5t+6=0$$ $$(t+2)(t+3)=0$$ So, $t=-2$ and $t=-3$ are points of discontinuity.
Thus, we solve $t^2+5t+6=0$ to find points of discontinuity: $$t^2+5t+6=0$$ $$(t+2)(t+3)=0$$ So, $t=-2$ and $t=-3$ are points of discontinuity.
b. Classify any discontinuity as jump, removable, infinite, or other.
We examine the limits of the function at both $t=-3$ and $t=-2.$
For $t=-3,$ $$\lim_{t \rightarrow -3}\frac{t+3}{t^2+5t+6}=\lim_{t \rightarrow -3}\frac{t+3}{(t+2)(t+3)}=\lim_{t \rightarrow -3}\frac{1}{t+2}=\frac{1}{3}.$$ Since the limit exists but there is no function value at $t=-3,$ this is a removable discontinuity.
For $t=-2,$ we notice that the left and right-hand limits are infinite: $$\lim_{t \rightarrow -2^-}\frac{t+3}{t^2+5t+6}=\lim_{t \rightarrow -2^-}\frac{1}{t+2}=-\infty$$ and $$\lim_{t \rightarrow -2^+}\frac{t+3}{t^2+5t+6}=\lim_{t \rightarrow -2^+}\frac{1}{t+2}=\infty$$ Thus, $t=-3$ is a removable discontinuity and and $t=-2$ is an infinite discontinuity.
For $t=-3,$ $$\lim_{t \rightarrow -3}\frac{t+3}{t^2+5t+6}=\lim_{t \rightarrow -3}\frac{t+3}{(t+2)(t+3)}=\lim_{t \rightarrow -3}\frac{1}{t+2}=\frac{1}{3}.$$ Since the limit exists but there is no function value at $t=-3,$ this is a removable discontinuity.
For $t=-2,$ we notice that the left and right-hand limits are infinite: $$\lim_{t \rightarrow -2^-}\frac{t+3}{t^2+5t+6}=\lim_{t \rightarrow -2^-}\frac{1}{t+2}=-\infty$$ and $$\lim_{t \rightarrow -2^+}\frac{t+3}{t^2+5t+6}=\lim_{t \rightarrow -2^+}\frac{1}{t+2}=\infty$$ Thus, $t=-3$ is a removable discontinuity and and $t=-2$ is an infinite discontinuity.
Continuity on an Interval
Definition: A function $f$ is continuous on an open interval $(a,b)$ if it is continuous at every point in $(a,b).$
Polynomials and Rational Functions
Theorem: Polynomials and rational functions are continuous at all points in their domains.
Example: Recall the function $\displaystyle f(t)=\frac{t+3}{t^2+5t+6}.$ Over what interval(s) is $f$ continuous?
By the above theorem, $f(t)$ is continuous in its domain. That is, $f(t)$ is continuous on
$$D=(-\infty,-3)\cup(-3,-2)\cup(-2,\infty).$$
Example: Consider the graph of a function $f$ below.
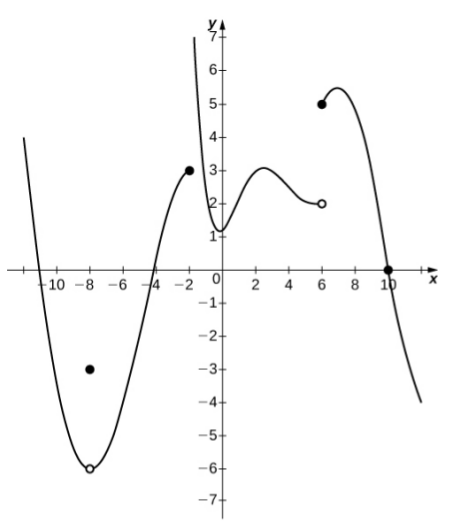
a. Find all values for which the function is discontinuous.
$f$ is discontinuous at $x=-8,$ $x=-2,$ and $x=6.$
b. Classify each discontinuity as either jump, removable, infinite, or other.
$x=-8$ is a removable discontinuity.
$x=-2$ is an infinite discontinuity.
$x=6$ is a jump discontinuity.
c. Over what interval(s) is the function continuous?
The function is continuous on $(-\infty,-8)\cup(-8,-2)\cup(-2,6)\cup(6,\infty)$
Question: What about closed intervals like $[a,b]$ and half-open intervals like $(a,b]$ and $[a,b)?$
Left and Right Continuity
A function $f(x)$ is said to be continuous from the right at $a$ if $\displaystyle \lim_{x \rightarrow a^+} f(x)=f(a).$
A function $f(x)$ is said to be continuous from the left at $b$ if $\displaystyle \lim_{x \rightarrow b^-} f(x)=f(b).$
Thus, for a function to be continuous on $[a,b],$ it must be continuous on $(a,b),$ right continuous at $a$ and left continuous at $b.$
Example
Over which interval(s) is the function $f(x)=\sqrt{x+3}$ continuous?
We consider $f$ over its domain $[-3,\infty).$ First, let $a \in (-3,\infty).$ Then, $$ \begin{array}{ll} \displaystyle \lim_{x \rightarrow a}f(x) & \mbox{}\\ =\displaystyle \lim_{x \rightarrow a}\sqrt{x+3} & \mbox{}\\ =\displaystyle \sqrt{\lim_{x \rightarrow a} (x+3)} & \mbox{A limit of a root is the root of the limit.} \\ =\sqrt{a+3} & \mbox{} \\ =f(a). & \mbox{} \\ \end{array} $$ Thus, $f$ is continuous on $(-3,\infty).$
We now verify that $f$ is continuous from the right at $x=-3:$ $$ \begin{array}{ll} \displaystyle \lim_{x \rightarrow -3^+}f(x) & \mbox{}\\ =\displaystyle \lim_{x \rightarrow -3^+}\sqrt{x+3} & \mbox{}\\ =\displaystyle \sqrt{\lim_{x \rightarrow -3^+} (x+3)} & \mbox{A limit of a root is the root of the limit.} \\ =\sqrt{0} & \mbox{} \\ =0 & \mbox{} \\ =f(-3) & \mbox{} \\ \end{array} $$ Since $f$ is also continuous from the right at $x=-3,$ $f$ is continuous on the interval $[-3,\infty).$
Composite Function Theorem
If $f(x)$ is continuous at $L$ and $\displaystyle \lim_{x→a}g(x)=L,$ then $$\displaystyle \lim_{x→a}f(g(x))=f\left(\lim_{x→a}g(x)\right)=f(L).$$
Trigonometric Functions
Theorem: Trigonometric functions are continuous at all points in their domains.
Example: Use the Composite Function Theorem to evaluate $\displaystyle \lim_{x \rightarrow \pi}\sin(x-\pi).$
$$
\begin{array}{ll}
\displaystyle \lim_{x \rightarrow \pi}\sin(x-\pi) & \mbox{}\\
=\sin\left(\displaystyle \lim_{x \rightarrow \pi}(x-\pi)\right) & \mbox{by the composite function theorem and that $y=\sin(x)$ is everywhere continuous} \\
=\sin(0) & \mbox{} \\
=0 & \mbox{} \\
\end{array}
$$
The Intermediate Value Theorem (IVT)
Let $f$ be continuous over a closed, bounded interval $[a,b].$ If $z$ is any real number between $f(a)$ and $f(b),$ then there is a number $c$ in $[a,b]$ such that $f(c)=z.$
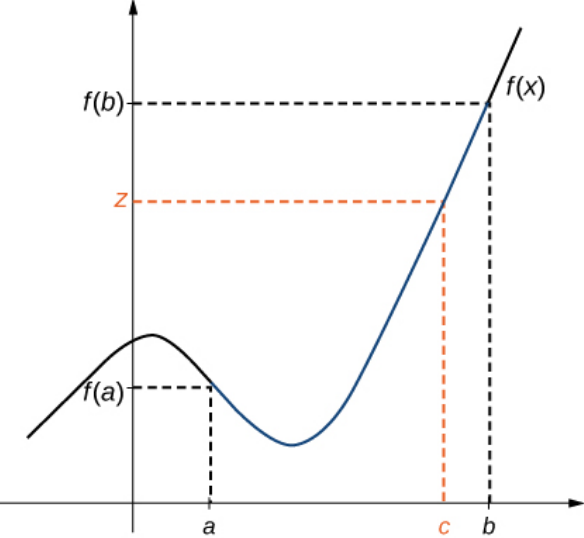
Remark: The IVT essentially says that a continuous function on $[a,b]$ hits all points between $f(a)$ and $f(b).$
The Intermediate Value Theorem (IVT)
Although the IVT may seem like an obvious statement, in reality it is difficult to prove.
In fact, our present definition of the limit is not enough to rigorously prove the IVT. (In the next section we will touch upon the rigorous definition of a limit.)
Moreover, there are many HUGE results in calculus which depend on the IVT. We are truly beginning to work at the foundations of the subject.
Finally, since most physical quantities such as position and speed are continuous (unless we teleport), there are physically meaningful results that we can extract from the IVT.
This is all to say the the IVT is a result worth knowing.
The Intermediate Value Theorem (IVT)
Even in its raw form, the IVT can exceedingly useful. For example, some applied problem might reduce to to finding the root of some polynomial in some interval.
The IVT can tell us when such a root exists.
Example: Show that $f(x)=x^3-x^2- 3x+ 1$ has a zero (root) over the interval $[0, 1].$
First we note that $f(0)=1$ and $f(1)=-2.$
Since $f$ is a polynomial, it is continuous on its entire domain.
Therefore, it is also continuous on $[0,1].$
Since $0$ is between $1$ and $-2,$ we may invoke the Intermediate Value Theorem to conclude that for some $c\in[0,1],$ we have $f(c)=0.$
That is, $f$ has a root in $[0,1].$
Since $f$ is a polynomial, it is continuous on its entire domain.
Therefore, it is also continuous on $[0,1].$
Since $0$ is between $1$ and $-2,$ we may invoke the Intermediate Value Theorem to conclude that for some $c\in[0,1],$ we have $f(c)=0.$
That is, $f$ has a root in $[0,1].$
Example
Consider the function $$ h(x)= \begin{cases} 3x^2-4, & x \leq 2 \\ 5+4x, & x \gt 2. \end{cases} $$ Over the interval $[0,4]$ there is no value of $x$ such that $h(x) = 10,$ even though $h(0) \lt 10 \lt h(4).$
Does this contradict the IVT?

Explanation of Grumpy Cat's Answer:
Note that the limit at $x=2$ does not exist since $\displaystyle \lim_{x\rightarrow 2^-}f(x)=8$ and $\displaystyle \lim_{x\rightarrow 2^+}f(x)=13.$
That is to say, $f$ is not continuous at $x=2.$
Thus, $f$ is not continuous on the entire interval $[0,4].$
Therefore, IVT does not apply, so there is no contradiction.
Dire Warning
If the conditions of the IVT are not met, then all bets are off.
That is, if a function $f$ is either:
1) not continuous on the interval being considered or
2) the interval considered is not closed and bounded,
then $f$ might hit all points in between $f(a)$ and $f(b),$ but then again, it might not.
In this situation there are no guarantees.
Consider the functions below defined on the interval $[2,4].$
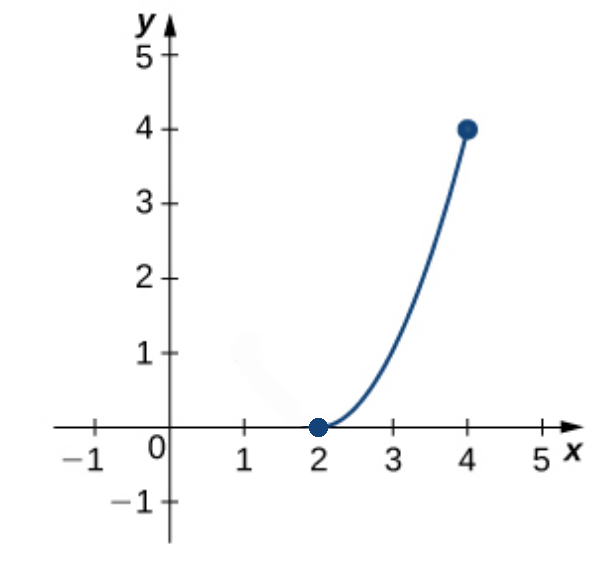 | 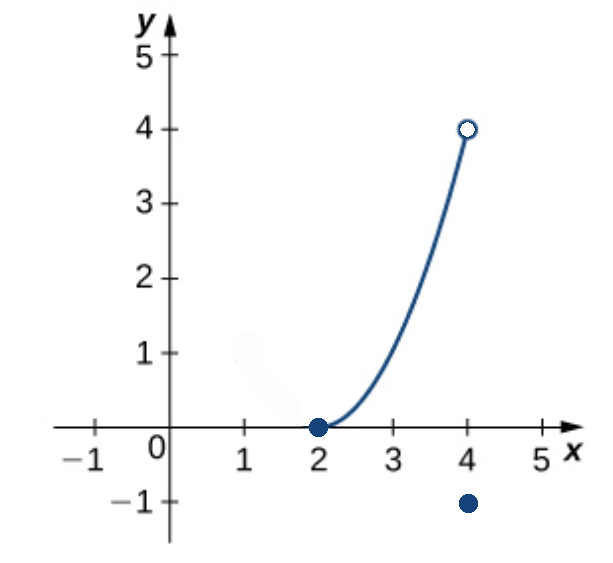 |  |
| IVT Applies | IVT Does Not Apply | IVT Does Not Apply |