We now begin with a truly fundamental notion which is the foundation all of calculus and many areas of advanced mathematics.
The limit of a function is the idea underpinning everything we study from here on out.
Limiting Behavior
Recall our Thought Experiment
Suppose we were to invest $\$1$ into a savings account which pays $100\%$ interest annually. After $1$ year we would have $\$2$ as seen in our table below.
| $n$ | $\displaystyle \left(1+\frac{1}{n}\right)^{n}$ |
The Limit of a Function
| $y=\displaystyle \frac{x^2-4}{x-2}$ | | |
| $x$ |
The Limit of a Function
Example: Since the $y$ values of the function $\displaystyle f(x)=\frac{x^2-4}{x-2}$ get closer and closer to $4$ as $x$ gets closer and closer to $2,$ we write $$\lim_{x\rightarrow 2}\frac{x^2-4}{x-2}=4.$$
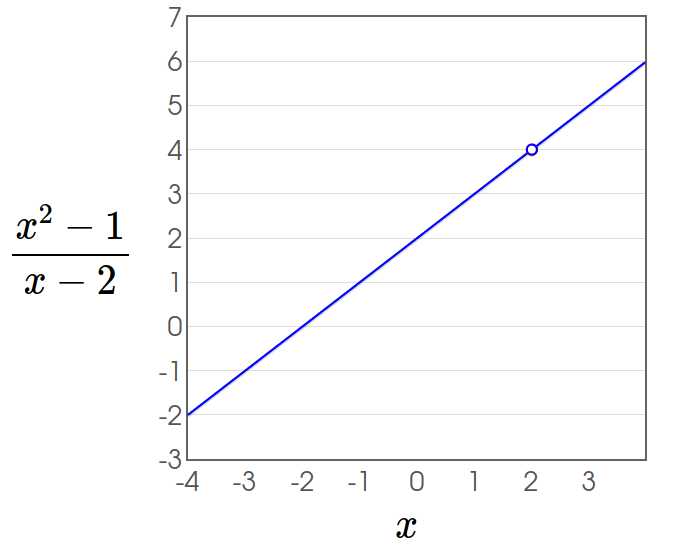
The Limit of a Function
We could have also used a table of values of $\displaystyle \frac{x^2-4}{x-2}$ as $x$ gets closer and closer to $2.$
| $x$ | $\displaystyle \frac{x^2-4}{x-2}$ |
The Intuitive Definition of a Limit
Let $f(x)$ be a function defined at all values in an open interval containing $a,$ with the possible exception of $a$ itself, and let $L$ be a real number. If all values of the function $f(x)$ approach the real number $L$ as the values of $x$ (not equal to $a$) approach the number $a,$ then we say that the limit of $f(x)$ as $x$ approaches $a$ is $L.$
Symbolically, we express this idea as $$\lim_{x \rightarrow a} f(x)=L.$$ More succinctly we may say that as $x$ gets closer to $a,$ $f(x)$ gets closer and stays close to $L.$
The Limit of a Function
Example: Estimate $\displaystyle \lim_{x \rightarrow 1} \frac{\frac{1}{x}-1}{x-1}$ using a table of functional values. Use a graph to confirm your estimate.
| $x$ | $\displaystyle \frac{\frac{1}{x}-1}{x-1}$ |
Limits Don't Always Exist
| $y=\displaystyle \frac{|x^2-4|}{x-2}$ | | |
| $x$ |
When a Limit Does Not Exist
Since the $y$ values of the function $\displaystyle f(x)=\frac{|x^2-4|}{x-2}$ do not get closer and closer to a single value as $x$ gets closer and closer to $2,$ we say that the limit $$\lim_{x\rightarrow 2}\frac{|x^2-4|}{x-2}$$ does not exist.
We may also write $\mbox{DNE}$ to say that "the limit does not exist."
One-Sided Limits: In applications it is common to restrict the domain of a function. For example, we might say that time is always greater than zero, or that distances cannot be negative. In this case, a one-sided limit may exist. For the example we considered above, both one-sided limits exist.
As $x$ approaches $2$ from the left-hand side, $\displaystyle f(x)=\frac{|x^2-4|}{x-2}$ approaches $-4.$
As $x$ approaches $2$ from the right-hand side, $\displaystyle f(x)=\frac{|x^2-4|}{x-2}$ approaches $4.$
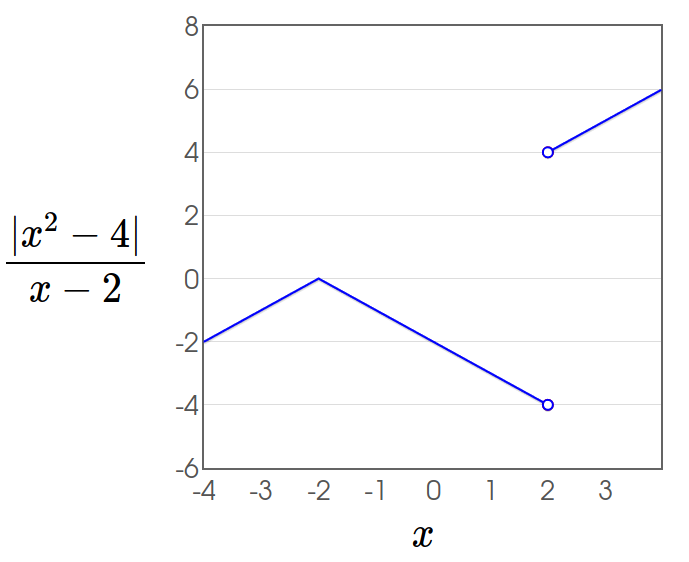
One-Sided Limits
For the left-sided limit we write $\displaystyle \lim_{x \rightarrow 2^{-}}\frac{|x^2-4|}{x-2}=-4$
For the right-sided limit we write $\displaystyle \lim_{x \rightarrow 2^{+}}\frac{|x^2-4|}{x-2}=4$

Limit from the Left
Let $f(x)$ be a function defined at all values in an open interval of the form $(c,a)$, and let $L$ be a real number. If the values of the function $f(x)$ approach the real number $L$ as the values of $x$ (where $x\lt a$) approach the number $a,$ then we say that $L$ is the limit of $f(x)$ as $x$ approaches $a$ from the left.
Symbolically, we express this idea as $$\lim_{x \rightarrow a^{-}} f(x)=L.$$ More succinctly we may say that as $x$ approaches $a$ from the left, $f(x)$ gets closer and stays close to $L.$
Limit from the Right
Let $f(x)$ be a function defined at all values in an open interval of the form $(a,c)$, and let $L$ be a real number. If the values of the function $f(x)$ approach the real number $L$ as the values of $x$ (where $x \gt a$) approach the number $a,$ then we say that $L$ is the limit of $f(x)$ as $x$ approaches $a$ from the right.
Symbolically, we express this idea as $$\lim_{x \rightarrow a^{+}} f(x)=L.$$ More succinctly we may say that as $x$ approaches $a$ from the right, $f(x)$ gets closer and stays close to $L.$
A Useful Theorem
Two-Sided limits and one-sided limits are related. Intuitively, it makes sense that if the left and right-hand limits exist, and both are the same value $L,$ then the two sided limit exists. Conversely, if the two-sided limit exists and is equal to $L,$ then the left and right-hand limits also exist and are equal to $L.$
Theorem
Let $f(x)$ be a function defined at all values in an open interval containing $a,$ with the possible exception of $a$ itself, and let $L$ be a real number. Then,
$\displaystyle \lim_{x \rightarrow a} f(x)=L$ if and only if $\displaystyle \lim_{x \rightarrow a^{+}} f(x)=L$ and $\displaystyle \lim_{x \rightarrow a^{-}} f(x)=L.$
Example
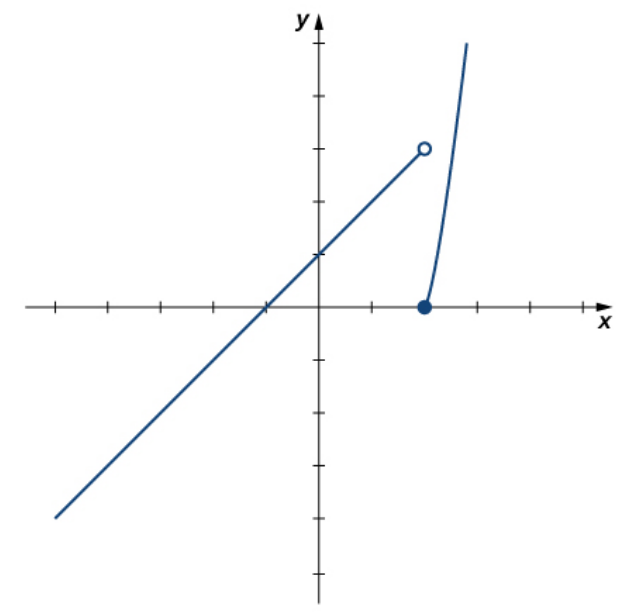
Let $f(x)=\begin{cases}x+1 \mbox{ if $x \lt 2$}\\ x^2-4 \mbox{ if $x \geq 2$}\end{cases}.$ Show that the limit $\displaystyle \lim_{x \rightarrow 2} f(x)$ does not exist.
From the graph we see that $\displaystyle \lim_{x \rightarrow 2^{-}} f(x)=3$ and $\displaystyle \lim_{x \rightarrow 2^{+}} f(x)=0.$
Since the left and right-hand limits are not equal, the two-sided limit $\displaystyle \lim_{x \rightarrow 2} f(x)$ does not exist.

Infinite Limits
Sometimes as we approach a value, the function values get either very large in the positive direction or the the negative direction.
Let's consider the behavior of the function $\displaystyle f(x)=\frac{1}{(x+1)^2}$ as $x$ approaches $-1.$
| $x$ | $\displaystyle \frac{1}{(x+1)^2}$ |
Infinite Limits
From the above we see that as $x$ approaches $-1$ from both the left and right-hand side, we can make $\displaystyle f(x)=\frac{1}{(x+1)^2}$ as large as we please.
In this case we have an infinite limit, and we may write $\displaystyle \lim_{x \rightarrow -1}\frac{1}{(x+1)^2}=\infty$
We also note that the left and right-hand limits are also infinite, that is
$\displaystyle \lim_{x \rightarrow -1^-}\frac{1}{(x+1)^2}=\infty$ and $\displaystyle \lim_{x \rightarrow -1^+}\frac{1}{(x+1)^2}=\infty$
Infinite Limits
The left and right-hand limits won't always agree as we have seen already.
Let's consider the behavior of another function $\displaystyle f(x)=\frac{1}{(x+1)^3}$ as $x$ approaches $-1.$
| $x$ | $\displaystyle \frac{1}{(x+1)^3}$ |
Infinite Limits
From the above we see that as $x$ approaches $-1$ from both the left, we can make $\displaystyle f(x)=\frac{1}{(x+1)^3}$ as large as we please in the negative direction. On the other hand, as $x$ approaches $-1$ from both the right, we can make $\displaystyle f(x)=\frac{1}{(x+1)^3}$ as large as we please in the positive direction. Thus, we may write
$\displaystyle \lim_{x \rightarrow -1^-}\frac{1}{(x+1)^3}=-\infty$ and $\displaystyle \lim_{x \rightarrow -1^+}\frac{1}{(x+1)^3}=\infty.$