Growth and decay are processes that occur in the study of life, finance, and other disciplines.
Exponential and logarithmic functions capture the most basic aspects of these phenomena.
Exponential Functions
Definition: the function $f(x)=b^x$ is called an exponential function.
Note: it will always be the case that $b>0.$
Basic Exponential Functions: Two Examples $$f(x)=3^x \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, g(x)=\left(\frac{1}{3}\right)^x$$
Example: Sketch a graph of the function $$f(x)=\left(\frac{1}{2}\right)^x$$ by complete the table of values and plotting points.
| $ \begin{array}{c|c} x & f(x) \\ \hline -2 & \\ -1 & \\ 0 & \\ 1 & \\ 2 & \\ \end{array} $ |  |
Example
Determine the equation of the exponential function graphed below.
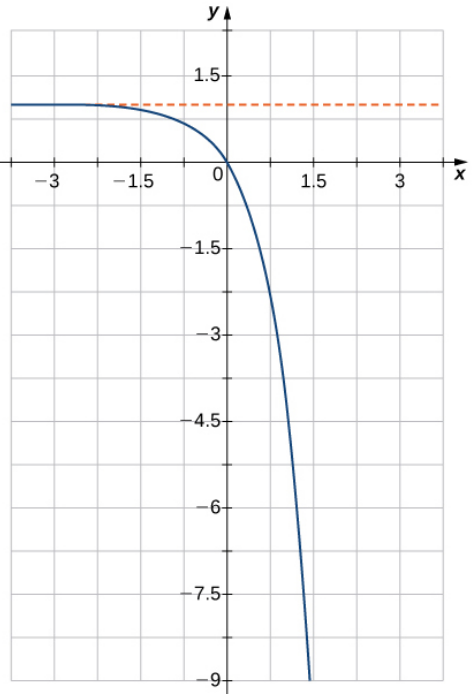
After a reflection over the $x$-axis and a horizontal shift up by $1,$ the function has the form, $f(x)=-b^x+1,$ or
$$f(x)=1-b^x.$$
From the graph, we know that $f(0.75)=-2.25.$ From this information we may find $b:$
$$1-b^{0.75}=-2.25.$$
Then $b^{3/4}=3.25$ so that
$$b=(3.25)^{4/3} \approx 4.814.$$
Thus, $$f(x) \approx 1-4.814^x$$
or alternatively
$$f(x)=1-\left(3.25^{4/3}\right)^x=1-3.25^{4x/3}.$$
A Fun Thought Experiment
Compound interest is computed using the formula $\displaystyle A=P\left(1+\frac{r}{n}\right)^{nt},$ where $t$ is the time in years, $A$ is the amount of money, $P$ is the principal amount, $r$ is the interest rate, and $n$ is the number of compounding periods per year.
Suppose we were to invest $\$1$ into a savings account which pays $100\%$ interest annually. After $1$ year we would have $\$2$ as seen in our table below.
| $n$ | $\displaystyle \left(1+\frac{1}{n}\right)^{n}$ |
A Very Special Base: The number $e$.
The base $e$ is an irrational number which is approximately equal to $2.718.$
This number is a "natural base" for many reasons which will become clearer later in the course.
Among these many reasons is that $e$ captures the notion of "continuous growth."
Any exponential function (growth or decay) can be written as $$A(t)=Ae^{rt}$$ where $A$ is an initial quantity and $r$ is the rate of increase or decrease.
Example
The strontium-$90$ in a nuclear reactor decays continuously. If $40$ mg is present initially, the amount present after $t$ years is given by $$A(t)=40e^{-0.0248t}.$$ Approximate to the nearest hundredth of a milligram the amount left after $80$ years.
$$A({\bf 80})=40e^{-0.0248*{\bf 80}} \approx 5.50.$$
That is, after $80$ years there will be about $5.5$ milligrams of strontium-$90$ remaining.
Logarithmic Functions
Definition: A logarithmic function is the inverse of an exponential function.
Example: $$f(x)=2^x \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, f^{-1}(x)=\log_2(x) \,\,\,\,\,$$
Logarithmic Functions
The functions $f(x)=2^x$ and $f^{-1}(x)=\log_2(x)$ are inverses of one another, so each is a reflection of the other over the line $y=x.$
Logarithms: The Big Idea
The following two equations are equivalent: $$y=b^x \,\,\,\,\,\,\,\,\,\,\,\,\, x=\log_b(y)$$ Notice: both of the above equations say the same thing: "$y$ has $x$ factors of $b$ in it."
Also Notice: Logarithms allow us to solve equations where the exponent is the variable.
Example: $8=2^3$ is equivalent to the expression $3=\log_2(8)$.
Another Way of Putting It
The notation $$\log_b(x)$$ asks the question: "What power of $b$ is $x?$"
Example: What question does $\log_3(27)$ ask? What is the answer?
Example: What question does $\log_4(2)$ ask? What is the answer?
Examples: Evaluate the following logarithmic expressions.
$\log_2 16$ $=4$
$\log_{4} 1$ $=0$
$\log_{10} 10$ $=1$
$\log_{3} \sqrt[3]{\frac{1}{27}}$ $=-1$
$\log_{10}0.0001$ $=-4$
Rewriting Equations
Remember: $y=b^x$ can always be rewritten as $x=\log_b(y)$, and vice versa.
Example: Convert the exponential equation to logarithmic form. $$4^{-3}=\frac{1}{64}.$$ Example: Convert the logarithmic equation to exponential form: $$\log_{3} \left(\frac{1}{9}\right)=-2.$$
Solving Equations
Remember: $y=b^x$ can always be rewritten as $x=\log_b(y)$, and vice versa.
Examples: Solve the following equations.
$\log_{4} x=2$ $\implies x=4^2=16$
$\log_{11} x=-\frac{1}{2}$ $\implies x=11^{-1/2}=\frac{1}{\sqrt{11}}\approx 0.301511345$
$\log_{x} 4=2$ $\implies 4=x^2 \implies x=2.$ (Logarithms can't have a negative base.)
Questions So Simple, They're Hard
Example: What question does $\log_3(3^3)$ ask? What is the answer?
Example: What question does $\log_{\frac{3}{4}}\left(\frac{3}{4}\right)^{-\frac{1}{3}}$ ask? What is the answer?
Consequence: A useful fact: $$\log_b (b^x)=x$$ Example: Evaluate $\log_{\gamma}\gamma^{\frac{1}{5}}$
Note: The above result simply reiterates that exponential and log functions are inverses of each other.
Graphs of Logarithmic Functions: Complete the table of values and use these points to sketch a graph of the function $$f(x)=\log_4(x).$$
| $\begin{array}{c|c}x & f(x) \\ \hline 1/4 & \\ 1 & \\ 4 & \\\end{array}$ |  |
Properties of Logarithms
Product Rule: $\log_b(xy)=\log_b(x)+\log_b(y)$
Quotient Rule: $\displaystyle \log_b\left(\frac{x}{y}\right)=\log_b(x)-\log_b(y)$
Power Rule: $\log_b(x^m)=m \log_b(x)$
Using Properties of Logarithms
Example: Use the properties of logarithms to express the logarithm in terms of logarithms of simpler expressions. $$\ln \frac{(13 \rho - 8)^{-2} (8 \mu + 11)^{4}}{(11 \tau - 15)^{3}}$$ $$ \begin{array}{lr} \displaystyle \ln \frac{(13 \rho - 8)^{-2} (8 \mu + 11)^{4}}{(11 \tau - 15)^{3}}&\\ =\ln ((13 \rho - 8)^{-2} (8 \mu + 11)^{4})-\ln((11 \tau - 15)^3)&\mbox{ by Quotient Rule}\\ =\ln ((13 \rho - 8)^{-2})+\ln((8 \mu + 11)^{4})-\ln((11 \tau - 15)^3)& \mbox{ by Product Rule}\\ =-2\ln (13 \rho - 8)+4\ln(8 \mu + 11)-3\ln(11 \tau - 15)& \mbox{ by Power Rule}\\ \end{array} $$
Dire Warning
WHEN YOU DO THIS
$\displaystyle \log_b(x+y)=\log_b(x)+\log_b(y)$
YOU MAKE KITTY ANGRY!!!!!!!!!!!!!!!!!!


Dire Warning
$\log_b(xy)$ is NOT equal to $\log_b(x)\log_b(y)$
$\log_b(x+y)$ is NOT equal to $\log_b(x)+\log_b(y)$
$\displaystyle \log_b\left(\frac{x}{y}\right)$ is NOT equal to $\frac{\log_b(x)}{\log_b(y)}$
$\log_b(x-y)$ is NOT equal to $\log_b(x)-\log_b(y)$

Using Properties of Logarithms
Example: Combine the logarithmic terms into a single logarithmic expression with a coefficient of 1. $$6 \log (a)+2\log (p)-8 \log (r)$$ $$ \begin{array}{lr} \displaystyle 6 \log (a)+2\log (p)-8 \log (r)&\\ =\log (a^6)+\log (p^2)- \log (r^8)&\mbox{ by Power Rule}\\ =\log (a^6 p^2)- \log (r^8)& \mbox{ by Product Rule}\\ =\displaystyle \log \left(\frac{a^6 p^2}{r^8}\right)& \mbox{ by Quotient Rule}\\ \end{array} $$
An Exceedingly Useful Property of Logarithms: The change of base formula. $$\log_b(x)=\frac{\log_a(x)}{\log_a(b)}.$$ Great News! We may now use our calculator to evaluate logarithms of any base!
Example: $\log_5 17$ $$ \log_5 17=\frac{\ln 17}{\ln 5}=\frac{\log 17}{\log 5}\approx 1.760374428 $$
Solving Exponential Equations:
Example: Find the exact solution to the equation. Express your answer in terms of base-$e$ logarithms. Then approximate your answer to the nearest hundredth. $$9^{6 x+7}=8$$ $$9^{6 x+7}=8$$ $$\ln\left( 9^{6 x+7} \right)=\ln(8)$$ $$(6 x+7)\ln\left( 9 \right)=\ln(8)$$ $$6 x+7=\frac{\ln(8)}{\ln\left( 9 \right)}$$ $$x=\frac{1}{6}\frac{\ln(8)}{\ln\left( 9 \right)}-\frac{7}{6}$$ $$x \approx -1.01$$ Scenic Alternative: Note that the exponential statement $9^{6 x+7}=8$ can simply be rewritten in logarithmic form: $$6 x+7=\log_9 8.$$ Then, $$6 x+7=\frac{\ln(8)}{\ln(9)}$$ using the change of base formula. You may then proceed as we did above.
Solving Logarithmic Equations
Example: Solve the logarithmic equation and round your answer to the nearest hundredth. $$\log_4(6 \theta +7)=-\frac{1}{2}$$ $$ \begin{array}{ll} \log_4(6 \theta +7)=-\frac{1}{2} &\mbox{}\\ 6 \theta +7=4^{-\frac{1}{2}}& \mbox{Rewrite log in exponential form.}\\ 6 \theta +7=\frac{1}{2}&\mbox{}\\ 6 \theta=-\frac{13}{2}&\mbox{}\\ \theta=-\frac{13}{12}&\mbox{}\\ \theta \approx -1.08&\mbox{}\\ \end{array} $$ Reminder: What is something we should do at this point?
Example: Solve the logarithmic equation and round your answer to the nearest hundredth. $$\log(x-2)-\log(x-5)=\log(x-7)$$ $$ \begin{array}{ll} \log(x-2)-\log(x-5)=\log(x-7) &\mbox{}\\ \displaystyle \log\left(\frac{x-2}{x-5}\right)=\log(x-7)& \mbox{using Quotient rule}\\ \displaystyle \frac{x-2}{x-5}=x-7&\mbox{using one-to-one property of logs}\\ \displaystyle x-2=(x-7)(x-5)&\mbox{}\\ \displaystyle x-2=x^2-12x+35&\mbox{FOILing out righthand expression}\\ \displaystyle x^2-13x+37=0&\mbox{getting everything to the other side}\\ \displaystyle x=\frac{-(-13) \pm \sqrt{(-13)^2-4\cdot 1 \cdot 37}}{2}&\mbox{using Quadratic Formula}\\ \displaystyle x=\frac{13 \pm \sqrt{21}}{2}&\mbox{}\\ \displaystyle x \approx 8.791287847 \mbox{ OR } x \approx 4.208712153 &\\ \end{array} $$ Reminder: What is something we should do at this point?
Dire Warning
WHEN YOU DON"T CHECK YOUR SOLUTIONS YOU MAKE KITTY ANGRY!!!!!!!!!!!!!!!!!!


Applications Of Exponential Equations
Most applications of exponential equations will be dealing with exponential functions of the form $$A(t)=A_0 e^{rt}.$$ Some problems will give you the initial amount $A_0$ of what is being studied (substance, people, money, etc.). and a rate of growth or decline $r.$ If it's a growth problem, $r$ is positive. If it's decay or decline, $r$ is negative.
Much of the time, we want to know the time at which them amount $A$ reaches some level. This will involve solving an exponential equation.
Modelling Population Growth
Example: The safe level of psychrotrophic bacteria in a gallon of milk is $100$ units. In a refrigerator set at $38^{\circ}\mbox{F},$ the number of units of these bacteria in a gallon of skim milk is approximated by the exponential function $$B(t)=4.0e^{0.24t},$$ where $t$ is the time in days. How long will it take the bacterial colony to grow to $160$ units? Round your answer to the nearest hundredth. $$ \begin{array}{ll} \displaystyle B(t)=160& \mbox{}\\ \displaystyle 4.0e^{0.24t}=160&\mbox{}\\ \displaystyle e^{0.24t}=40&\mbox{}\\ \displaystyle 0.24t=\ln(40)&\mbox{}\\ \displaystyle t=\frac{\ln 40}{0.24}&\mbox{}\\ \displaystyle t \approx 15.37 &\mbox{}\\ \end{array} $$ That is, it will take about $15.37$ days for the the level of bacteria to reach $160$ units.
A Graphical Approach
$y=160\,\,\,\,\,\,\,\,\,\,\,\,\,$ $y=4.0e^{0.24t}$
Application of Logarithmic Equations: The pH of a Chemical Solution
Example: The formula $\mbox{pH}=-\log \mbox{H}^+$ expresses the $\mbox{pH}$ of a solution in terms of its hydrogen ion concentration $\mbox{H}^+.$ A certain brand of shampoo has a $\mbox{pH}$ of $8.72.$ What is the $\mbox{H}^+$ concentration in moles per liter? $$ \begin{array}{ll} \displaystyle \mbox{pH}=-\log \mbox{H}^+& \mbox{start with general equation}\\ \displaystyle 8.72=-\log \mbox{H}^+&\mbox{plug in known info}\\ \displaystyle -8.72=\log \mbox{H}^+&\mbox{}\\ \displaystyle \mbox{H}^+=10^{-8.72}&\mbox{rewrite logarithmic statement as an exponential statement}\\ \displaystyle \mbox{H}^+ \approx 0.000000002&\mbox{}\\ \end{array} $$ The concentration of $\mbox{H}^+$ ions is about $0.000000002$ moles per liter.