The Big Idea: Inverse functions "undo" what another function does.
Example: If $f$ sends $-2$ to $3$ (i.e., $f(-2)=3$), then the inverse function, $f^{-1},$ sends $3$ back to $-2$, (i.e., $f^{-1}(3)=-2$).
Another Example: Consider the function $f$ and its inverse $f^{-1}$ below.
$\begin{array}{c|c}x & y=f(x) \\ \hline y & \blacklozenge \\ d & -\pi \\ \blacklozenge & \flat \\ -\pi & \lozenge \\ \end{array}
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\begin{array}{c|c}x & y=f^{-1}(x) \\ \hline \blacklozenge & y \\ -\pi & d \\ \flat & \blacklozenge \\ \lozenge & -\pi \\ \end{array}$
Recall: a function is just a collection of ordered pairs. Notice that the table of ordered pairs for $f^{-1}$ is simply the reverse of those of $f$.
Notation: The function $$\begin{array}{c|c}x & y=f(x) \\ \hline y & \blacklozenge \\ d & -\pi \\ \blacklozenge & \flat \\ -\pi & \lozenge \\ \end{array}$$ may also be written explicitly as a collection of ordered pairs: $$f=\{(y, \blacklozenge), (d,-\pi), (\blacklozenge, \flat), (-\pi, \lozenge) \}.$$
Warning: The inverse relation of a function is not always a function.
Example: Consider the function below. Its inverse relation IS NOT a function. $$\begin{array}{c|c}x & y=f(x) \\ \hline x & x \\ e & e \\ \pi & x \\ y & e \\ \end{array}$$
Another Example
Consider the function $f(x)=2x+3$.
Verbally, this function "multiplies by $2,$ and then adds $3.$"
To "undo" what this function does, "subtract $3,$ and then divide by $2.$"
That is, the inverse function is $\displaystyle f^{-1}(x)=\frac{x-3}{2}.$
Notice: for example $f(3)=2\cdot 3+3=9$, and $\displaystyle f^{-1}(9)=\frac{9-3}{2}=3.$
Process to algebraically find the inverse of a function:
1) Swap $x$ and $y$
2) Solve for $y$
Example: Algebraically find the inverse of the function $$y=f(x)=\sqrt[3]{x-3}+2$$
Graphs of Inverse Functions: An example. $$f(x)=\sqrt[3]{x-3}+2 \,\,\,\,\ \mbox{ (blue)}\,\,\,\,\,\,\,\,\,\,\,\,\, f^{-1}(x)=(x-2)^3+3 \,\,\,\,\ \mbox{ (red)}$$
Big Question: How do I know if a function has an inverse?
Big Answer: If it's one-to-one.
Definition: a function is one-to-one is every $x$ maps to one and only one $y.$
Example : The function on the left is one-to-one, but the function on the right is not one-to-one. $$ \begin{array}{c|c}x & y=f(x) \\ \hline \blacktriangle & \lozenge \\ \clubsuit & \flat \\ \lozenge & e \\ \flat & \pi \\ \end{array} \,\,\,\,\,\,\,\,\,\, \begin{array}{c|c}x & y=f(x) \\ \hline x & x \\ e & e \\ \pi & x \\ y & e \\ \end{array} $$
Big Question: Can we tell if a function is one-to-one from its graph?
Big Answer: Yes! If it passes the "horizontal line test."
Graphs of One-to-One Functions
Example: The graphs of all the following functions are one-to-one since they pass the horizontal line test. Therefore, their inverse relations are also functions.
Graphs which ARE NOT One-to-One Functions
Example: The graphs of all the following functions ARE NOT one-to-one since they fail the horizontal line test. Therefore, their inverse relations ARE NOT functions.
A More Formal Definition of One-To-One
A function $f$ is one-to-one provided that whenever $f(x_1)=f(x_2),$ then $x_1=x_2.$
Example: Show formally that the function $f(x)=\sqrt[3]{x-3}+2$ is one-to-one.
Fun Fact: Compositions of inverses always return $x$. In symbols $$(f \circ f^{-1})(x)=x \mbox{ and } (f^{-1} \circ f)(x)=x.$$
Example: Consider the tables $\begin{array}{c|c}\hline x & f^{-1}(x) \\ \hline 9 & 2\\ \hline -5 & -6\\ \hline -7 & 0\\ \hline\end{array}$ and $\begin{array}{c|c}\hline x & f(x) \\ \hline 2 & 9\\ \hline -6 & -5\\ \hline 0 & -7\\ \hline\end{array}$
Find the table for $f \circ f^{-1}.$
Example: For $f(x)=\sqrt[3]{x-3}+2$ and $f^{-1}(x)=(x-2)^3+3,$ find $f \circ f^{-1}.$
Constructing Inverses by Restricting the Domain
You often hear the "squaring" and "taking square roots" are inverse processes. This is not entirely true since since the inverse relation of $f(x)=x^2$ is not a function. To get the "inverse of the squaring function," that is, the square root function, we must restrict the domain of $f$ to the interval $[0,\infty)$
| $f(x)=x^2$ and its inverse relation | $f(x)=x^2$ with restricted domain and its inverse function $g(x)=\sqrt{x}$ |
Inverse Trig Functions
The trig functions miserably fail the horizontal-line test. But we can restrict their domains to construct the inverse trig functions.
Inverse Trig Functions
The trig functions miserably fail the horizontal-line test. But we can restrict their domains to construct the inverse trig functions
Inverse Trig Functions
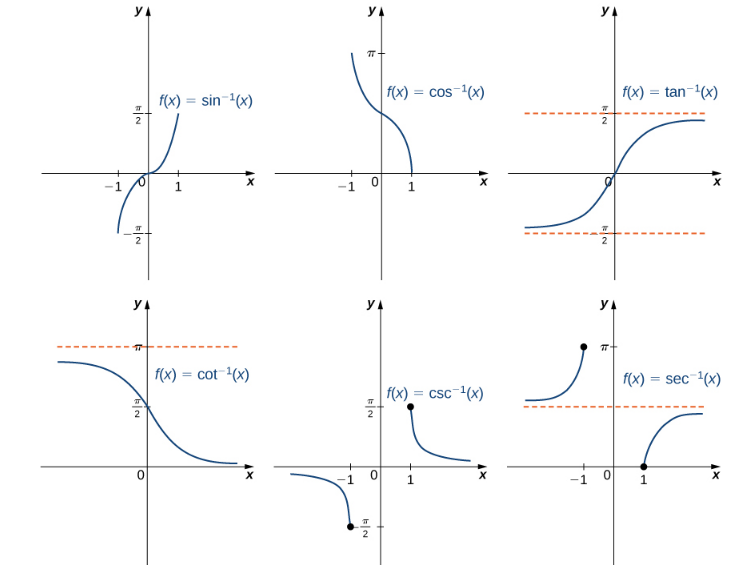
Inverse Trig Functions
Examples: Evaluate the function. Give the exact value.
$\displaystyle \cot^{-1}(1)$
$\displaystyle \cos\left(\tan^{-1}\left(\sqrt{3}\right)\right)$
Application: Inverse Trig Functions
An airplane’s Mach number $M$ is the ratio of its speed to the speed of sound. When a plane is flying at a constant altitude, then its Mach angle is given by $μ = 2 \sin^{-1}\left( \frac{1}{M} \right) .$
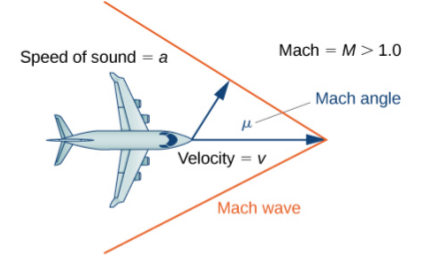
Find the Mach angle $\mu$ (to the nearest degree) for the following Mach numbers.
a. $M=1.4$
b. $M=2.8$