We've seen how even simple functions can model certain patterns well.
The trigonometric functions model periodic patterns.
Radian Measure
When solving triangles, we often use degree measure, but radian angle measure is analytically a much more natural way to measure angles.
This will statement will become more apparent when we start doing calculus operations on trig functions.
Recall: An angle $\theta$ measured in radians defined to be the arc length on the unit circle swept out by $\theta.$ (This is the number of radii swept out by $\theta$ on a circle of any radius, hence the name radians.)
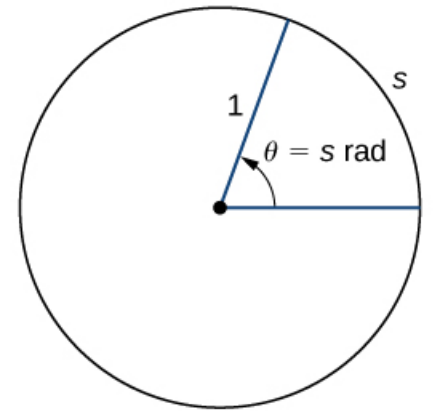
Converting Between Radians and Degrees
Both measures are common enough that it is sometimes necessary to be able to convert between both.
Treating angles as units of measure, the conversion $\pi \mbox{ rad}=180^{\circ}$ enables us to convert between radians and degrees, and vice versa.
Example: Express $210^{\circ}$ using radians. $$\displaystyle 210^{\circ} \cdot \frac{\pi \mbox{ rad}}{180^{\circ}}=\frac{7\pi}{6} \mbox{ rad}$$ Example: Express $11\pi/6 \mbox{ rad}$ using degrees. $$\displaystyle \frac{11\pi}{6} \mbox{ rad} \cdot \frac{180^{\circ}}{\pi \mbox{ rad}}=330^{\circ}$$
Analytic Definitions of the Six Basic Trig Functions
With radian angle measure, we may now define the six trigonometric functions.
Suppose the point $(x,y)$ is the point on the unit circle that sweeps out an angle $\theta$ as seen below.
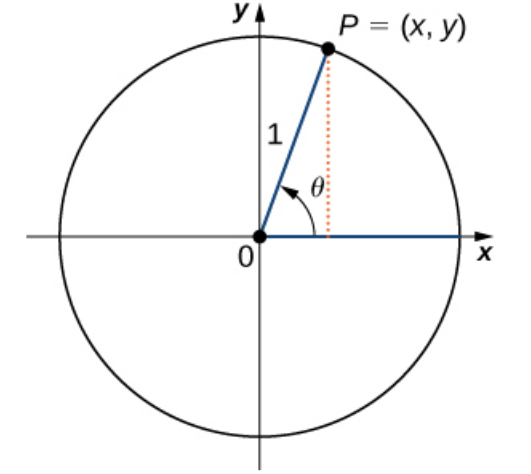
$\displaystyle \sin \theta =\frac{\mbox{opposite}}{\mbox{hypotenuse}}=\frac{y}{1}=y$ ($\sin \theta$ is just the $y$-coordinate)
$\displaystyle \cos \theta =\frac{\mbox{adjacent}}{\mbox{hypotenuse}}=\frac{x}{1}=x$ ($\cos \theta$ is just the $x$-coordinate)
$\displaystyle \tan \theta =\frac{\mbox{opposite}}{\mbox{adjacent}}=\frac{y}{x}$
The Other Three Ratios
The other three trigonometric ratios can then be defined in terms of the basic three above:
$$\displaystyle \cot \theta =\frac{1}{\tan \theta}$$ $$\displaystyle \sec \theta =\frac{1}{\cos \theta}$$ $$\displaystyle \csc \theta =\frac{1}{\sin \theta}$$
Evaluating Trig Functions
Example: Evaluate $\displaystyle \cos\left(\frac{3\pi }{4}\right).$


Example: Evaluate $\displaystyle \tan\left(\frac{7\pi }{3} \right).$

Right Triangle Trig: Using the more rigorous definitions from above, we can still do right triangle trig:
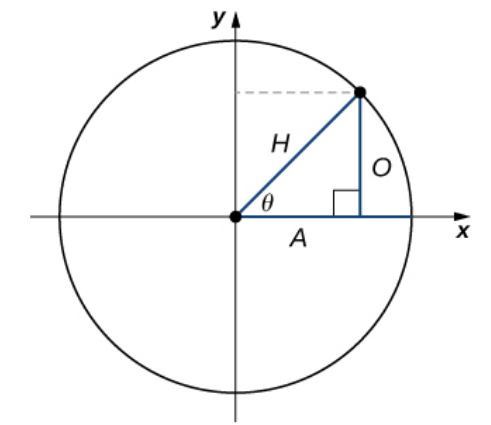
$\displaystyle \sin \theta =\frac{\mbox{O}}{\mbox{H}},$ $\,\,\,\,\displaystyle \csc \theta =\frac{\mbox{H}}{\mbox{O}}$
$\displaystyle \cos \theta =\frac{\mbox{A}}{\mbox{H}},$ $\,\,\,\,\displaystyle \sec \theta =\frac{\mbox{H}}{\mbox{A}}$
$\displaystyle \tan \theta =\frac{\mbox{O}}{\mbox{A}},$ $\,\,\,\,\displaystyle \cot \theta =\frac{\mbox{A}}{\mbox{O}}$
Example: A house painter wants to lean a $20$-foot ladder against a house. If the angle between the base of the ladder and the ground is to be $60^{\circ},$ how far from the house should she place the base of the ladder?
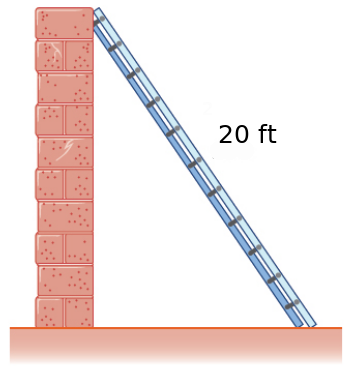
$$\displaystyle \cos(60^{\circ})=\frac{\mbox{A}}{\mbox{H}}=\frac{x}{20}.$$ Then, $$\displaystyle x=20\cos(60^{\circ})=20 \cdot \frac{1}{2}=10.$$ So, the base of the ladder should be placed $10$ feet away from the house.
Trig Identities
As we proceed through not only this course, but subsequent courses as well (MTH 252 and 253 for example), I cannot overstate the importance of being nimble with identities.
Some identities you may need to look up again and that's fine, but some you should be able to derive from the basic definitions that we've talked about so far.
In particular these identities should should be at the tip of your brain at all times:
Basic/Reciprocal: $\,\,\,\,\displaystyle \tan \theta =\frac{\sin \theta}{\cos \theta},$ $\,\,\,\,\displaystyle \cot \theta =\frac{1}{\tan \theta},$ $\,\,\,\,\displaystyle \sec \theta =\frac{1}{\cos \theta},$ $\,\,\,\,\displaystyle \csc \theta =\frac{1}{\sin \theta}$
Pythagorean: $\,\,\,\,\displaystyle \sin^2 \theta+\cos^2 \theta =1,$ $\,\,\,\,\tan^2 \theta+1=\sec^2 \theta,$ $\,\,\,\,\displaystyle 1+\cot^2 \theta=\csc^2 \theta$
Trig Identities
Other identities you may need to look up.
Sum and Difference: $$\,\,\,\,\sin(α±β)= \sin α\cos β±\cosα\sinβ,$$ $$\,\,\,\,\displaystyle \cos(α±β) = \cosα\cosβ∓ \sinα\sinβ$$ Double-Angle: $$\sin(2θ)= 2\sinθ\cosθ$$ $$\cos(2θ)= 2\cos^2θ- 1 = 1 - 2\sin^2θ= \cos^2θ- \sin^2θ$$ For the Future: The above give two useful forms which we will use in MTH 252: $$\displaystyle \cos^2 \theta=\frac{1+\cos(2 \theta)}{2} \,\,\, \mbox{ and } \,\,\,\displaystyle \sin^2 \theta=\frac{1-\cos(2 \theta)}{2}.$$
When We Use Identities
#1) To perform calculus operations.
#2) After applying calculus operations on trig functions, we will often need to solve equations involving trig functions.
Example: Find all solutions to the equation $\cos(2θ)= \sinθ.$
#3) To prove other identities that make calculations simpler.
Example: Prove the trigonometric identity $\displaystyle \frac{\sin x}{\cos x+1}+\frac{\cos x-1}{\sin x}=0.$
$$
\begin{array}{rl}
\displaystyle \frac{\sin x}{\cos x+1}+\frac{\cos x-1}{\sin x}&=\displaystyle\frac{\sin x \cdot \color{magenta}{\sin x}}{(\cos x+1)\color{magenta}{\sin x}}+\frac{(\cos x-1)\color{magenta}{(\cos x+1)}}{\sin x\color{magenta}{(\cos x+1)}}\\
&=\displaystyle\frac{\sin^2 x}{\sin x (\cos x+1)}+\frac{\cos^2 x-1}{\sin x (\cos x+1)}\\
&=\displaystyle\frac{\sin^2 x+\cos^2 x-1}{\sin x (\cos x+1)}\\
&=\displaystyle\frac{1-1}{\sin x (\cos x+1)}\\
&=0\\
\end{array}
$$
Graphs of Trig Functions
Trig functions are very good at modelling phenomena that are periodic. For example:
- Vibrations, signals, and sounds, etc.
- Seasonal cycles in temperature, sizes of animal populations, hours of daylight at a given time of year, etc.
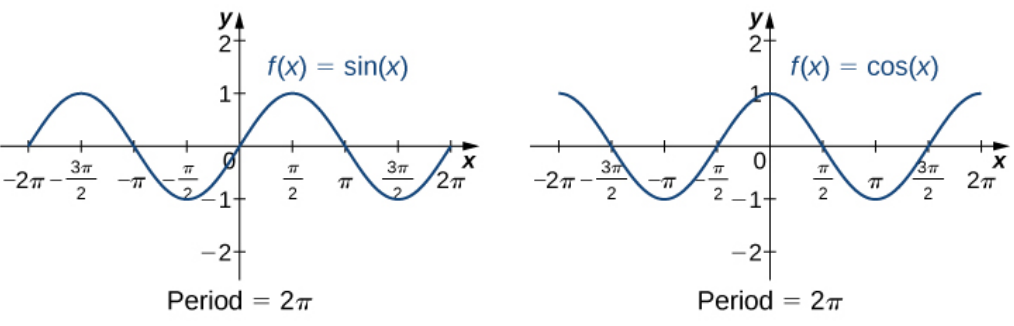
Graphs of Trig Functions
The sine and cosine graphs are a direct result of their definition in terms of the unit circle.
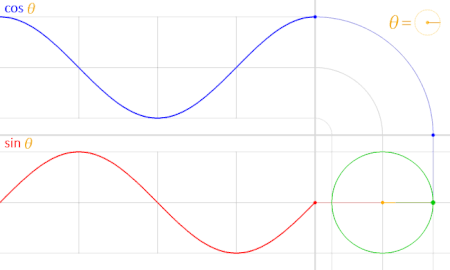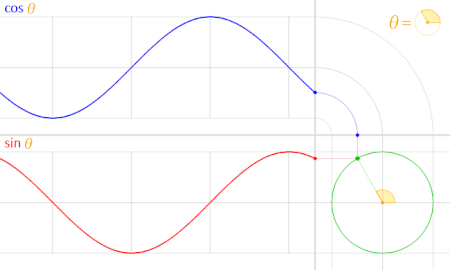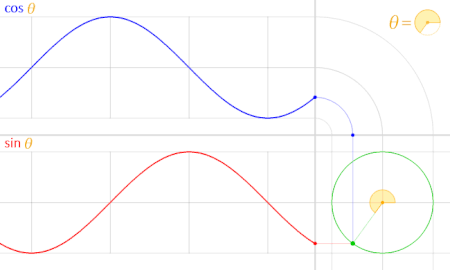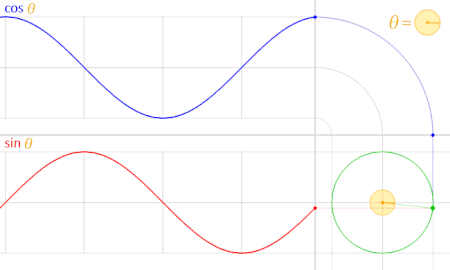
Graphs of Trig Functions
Trig functions are periodic. That is the pattern repeats over and over again.
The formal way to say that a function has period $p$ if $p$ is the smallest number such that is $f(x)=f(x+p)$ for all $x.$
For example, the sine and cosine functions have period $2\pi$ since $\sin(x)=\sin(x+2\pi)$ and $\cos(x)=\cos(x+2\pi).$ That is a shift to the left by $2\pi$ results in the same graph.

Graphs of Trig Functions
The following are the graphs of the other four trig functions. These can all be understood in terms of their unit circle definitions.

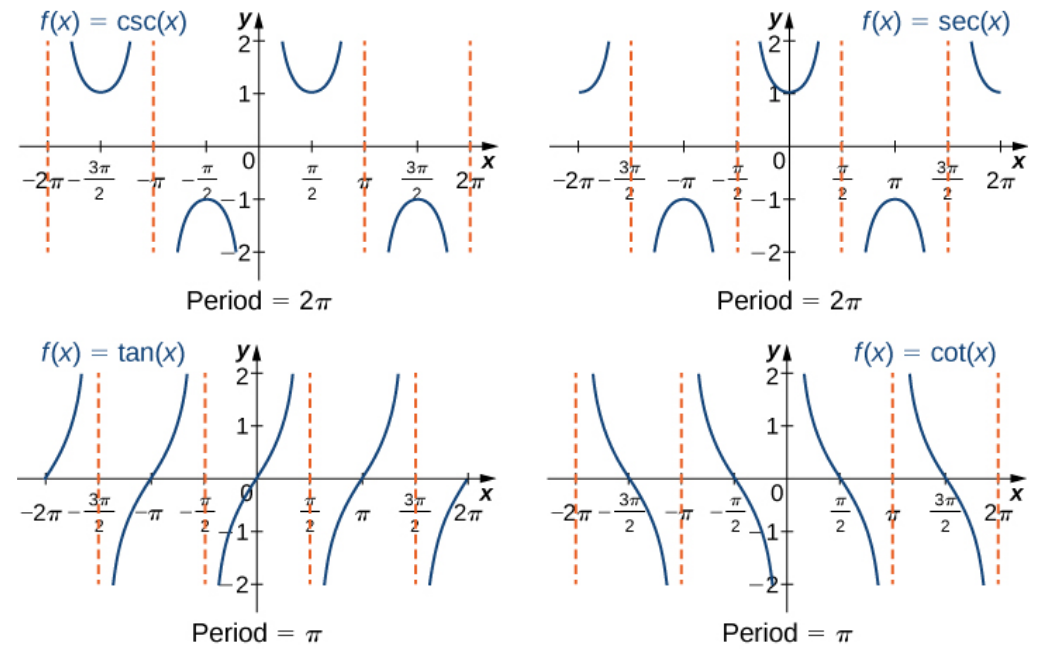
Graphs of Trig Functions
The graphs of $y=\csc x,$ $y=\sec x,$ and $y=\cot x$ can be understood as reciprocals $y=\sin x,$ $y=\cos x,$ and $y=\tan x,$ respectively.
| $y=\sin(x)$ $y=\csc(x)$ | $y=\cos(x)$ $y=\sec(x)$ | $y=\tan(x)$ $y=\cot(x)$ |
Graphing Trig Functions
There are plenty of useful trig functions we may graph and understand using the idea of transformations. Every sinusoidal curve can be thought of as having the form $f(x)=A\sin(B(x-\alpha))+C.$
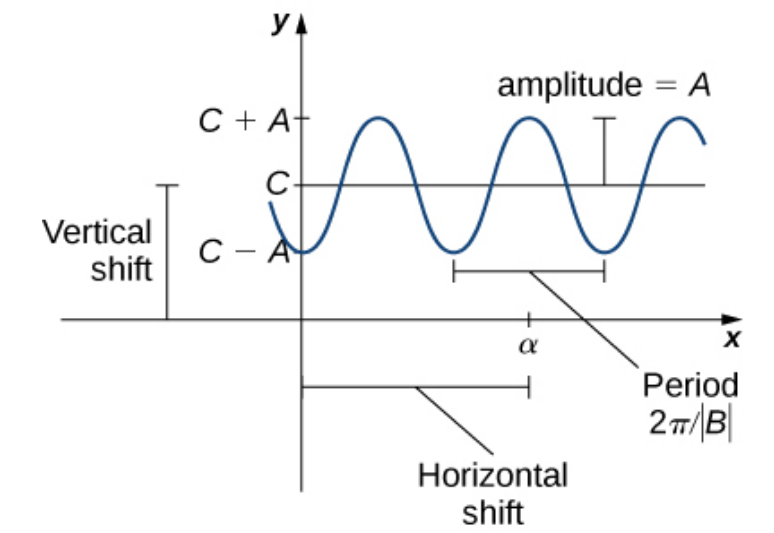
Graphing Trig Functions
Example: Sketch a graph of the function $\displaystyle f(x)=3\sin\left(2x-\frac{\pi}{2}\right)-4.$
Graphing Trig Functions
Example: Write the equation of the function graphed below in the form $f(x)=A\sin(B(x-\alpha))+C.$
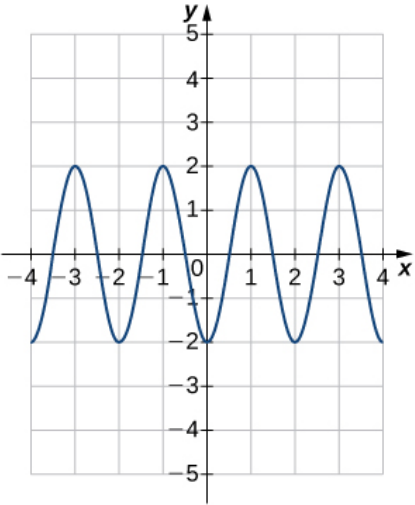
1) The amplitude is $2$ so that $A=2.$
2) The period is $2$. Thus, $\displaystyle \frac{2\pi}{|B|}=2$ which gives $|B|=\pi.$ Choosing the positive root, we have $B=\pi.$
3) The vertical shift is $0$ so that $C=0.$
4) The horizontal shift is $\displaystyle \alpha=\frac{1}{2}.$
From the above facts we have $\displaystyle f(x)=2\sin\left(\pi\left(x-\frac{1}{2}\right)\right).$
If There's Time... An Application
The graph below is a sinusoidal fit of the average-high-temperature data from my hometown. The red function $T(t)$ is given by $$T(t)= 19.5379·\sin(0.5236t−1.7337) + 72.9917$$ Use the function $T$ to estimate at what time(s) the average high temperature reaches $80^{\circ}$ Fahrenheit.
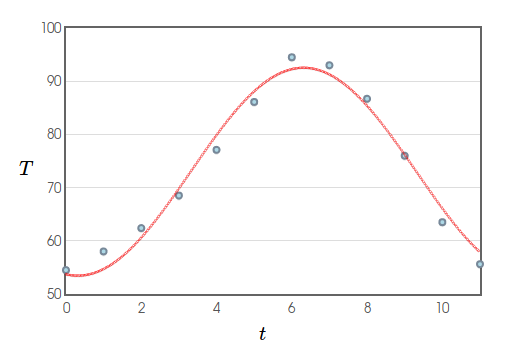
The question at this point is for what values $\theta$ between $-1.7337$ and $4.5495$ does $\sin(\theta)$ equal $0.3587?$
As a preview to inverse trig functions, $\sin^{-1}(0.3587)\approx 0.3668778721.$
It must be, then, that $$0.5236t−1.7337=0.3668778721$$ or $$0.5236t−1.7337=\pi-0.3668778721=2.7747178122.$$ So, the average temperature hits $80^{\circ}$ Fahrenheit at about $t \approx 4.0$ months and $t\approx 8.6$ months.