Recall Big-Time-Super-Important Vocab:
A parameter is a numerical fact about a population.
A statistic is a value we compute from a sample of our population.
Drawing conclusions about a population from a sample is called...
Estimating Parameters: Confidence Intervals
We are now beginning to ride the crest of the statistical wave, folks!
We know how to compute sample means, but how do we know how good our estimate is?
Estimating Parameters: Confidence Intervals
When we estimate a parameter with a sample statistic (in this case, the sample mean), we want to know how good our estimate is.
So we construct an interval that captures the true parameter a known percentage the time (i.e, with a known probability).
The interval has the form $$\mbox{estimate} \pm \mbox{margin of error}$$ The details of calculating the margin of error will be one of the focuses of this course.
Calculating the Margin of Error
Suppose we draw a simple random sample of size $n$ from a population with mean $\mu$ and standard deviation $\sigma$.
Big Question: Who remembers how the sample means $\bar{x}$ are distributed?
Recall: The Central Limit Theorem
Draw an SRS of size $n$ from any population with mean $\mu$ and standard deviation $\sigma.$ The central limit theorem says that when $n$ (the sample size) is large, the sampling distribution of the sample means $\bar{x}$ is approximately normal with distribution with mean $\mu$ and standard deviation $\frac{\sigma}{\sqrt{n}}.$ That is, $$\bar{x} \sim N\left(\mu,\frac{\sigma}{\sqrt{n}}\right).$$
Let's draw a normal curve with mean $\mu$ and standard deviation $\sigma/\sqrt{n}$.

$$P\left(\mu-2\frac{\sigma}{\sqrt{n}}<\bar{x}<\mu+2\frac{\sigma}{\sqrt{n}}\right) \approx 0.95.$$
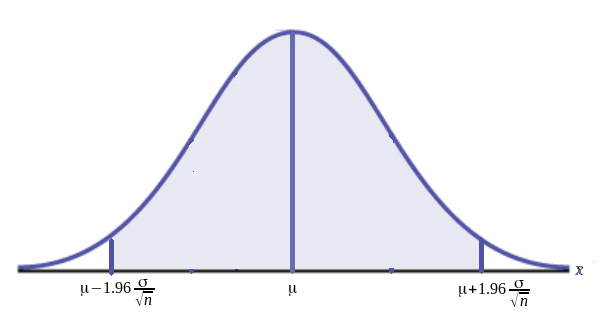
$$P\left(\mu-1.96\frac{\sigma}{\sqrt{n}}<\bar{x}<\mu+1.96\frac{\sigma}{\sqrt{n}}\right)=0.95.$$
Performing some algebraic shenanigans on the above, this is equivalent to
$$P\left(\bar{x}-1.96\frac{\sigma}{\sqrt{n}}<\mu<\bar{x}+1.96\frac{\sigma}{\sqrt{n}}\right)=0.95$$
HUGE Question What is the significance of the above probability statement????
HUGE Answer: The value $\displaystyle 1.96\frac{\sigma}{\sqrt{n}}$ is the margin of error for the $95\%$ confidence interval!
In other words: when we calculate the sample mean $\bar{x}$, there is a $95\%$ chance that the true population mean $\mu$ is between the values $$\bar{x}-1.96\frac{\sigma}{\sqrt{n}} \mbox{ and } \bar{x}+1.96\frac{\sigma}{\sqrt{n}}.$$
Important Vocab and Notation:
Draw a simple random sample of size $n$ from a population with mean $\mu$ and standard deviation $\sigma$, then the $95\%$ confidence interval for the mean $\mu$ is
$$\left(\bar{x}-1.96\frac{\sigma}{\sqrt{n}}, \bar{x}+1.96\frac{\sigma}{\sqrt{n}}\right).$$
Example:
Below is the height of all the citizens of Squaresville.
The true mean height is $\mu=$ and standard deviation $\sigma=$.
Let's suppose that we don't know this and sample
citizens to estimate the true mean height with the $95\%$ confidence interval $\color{red}{\displaystyle \left(\bar{x}-1.96\frac{\sigma}{\sqrt{n}}, \bar{x}+1.96\frac{\sigma}{\sqrt{n}}\right)}.$
A Kind of Pesky Question: What if we wanted a $99\%$ confidence interval?
A Sort of Nice Answer: We wouldn't have used the value of $1.96$ in our calculation. Instead, we would have used $2.576$.
Why, you ask? Because on a standard normal curve $99\%$ percent of all observations lie between $-2.576$ and $2.576$.
The value of $z$ on the standard normal table which which captures some percentage (i.e., $95\%,$ $99\%,$ etc.) of all values is denoted $z^*$.
Example: Below is the height of all the citizens of Squaresville. The true mean height is $\mu=$ and standard deviation $\sigma=$. Let's suppose that we don't know this and sample citizens to estimate the true mean with the $99\%$ confidence interval $\color{red}{\displaystyle \left(\bar{x}-2.576\frac{\sigma}{\sqrt{n}}, \bar{x}+2.576\frac{\sigma}{\sqrt{n}}\right)}.$
A modest table of values of $z^*$: $$ \begin{array}{c|cc} \hline \mbox{Confidence Level $C$} & 90\% & 95\% & 99\%\\ \hline \mbox{Critical Value $z^{*}$} & 1.645 & 1.96 & 2.576 \\ \hline \end{array} $$
General Confidence Interval
Choose the value of $z^*$ corresponding to $C\%$, and the $C\%$ confidence interval is $$\left(\bar{x}-z^{*}\frac{\sigma}{\sqrt{n}}, \bar{x}+z^{*}\frac{\sigma}{\sqrt{n}}\right).$$
A Truly Pesky Question: We don't know $\mu$. How do we know $\sigma$?
One More (I promise) Irritating Question: Are the $\bar{x}$'s exactly normally distributed?
CLT starts to really kick in at about $n>40$, so these calculations really require larger sample sizes to be considered trustworthy.
Otherwise, if your sample size is less than $40,$ you need to convince yourself and your readers that your simple random sample came from a normally distributed population.
Example: The following are a random sample of $n=31$ IQ scores of seventh-grade students from a school district in Portland: $$ 114, 100, 108, 130, 111, 103, 104, 89, 102, 91,\\ 120, 132, 111, 128, 74, 112, 107, 103, 114, 118,\\ 98, 114, 119, 96, 103, 86, 112, 105, 72, 112, 93 $$ It is not entirely unreasonable to use $\sigma=15$ as the population standard deviation since this is the standard deviation of all IQ scores.
Use these data to calculate a $90\%,$ $95\%,$ and a $99\%,$ confidence interval for the true mean IQ $\mu$ for this population.
The above data set contains $n=31$ data points, and $\bar{x}=105.839$ to 3 decimal places.
To calculate our $90\%$ confidence interval, we use $z^{*}=1.645.$ Then $$ \begin{array}{ll} &\left(\bar{x}-z^{*}\frac{\sigma}{\sqrt{n}}, \bar{x}+z^{*}\frac{\sigma}{\sqrt{n}}\right)\\ =&\left(105.839-1.645\frac{15}{\sqrt{31}}, 105.839+1.645\frac{15}{\sqrt{31}}\right)\\ =&(101.407,110.271) \end{array} $$
To calculate our $95\%$ confidence interval, we use $z^{*}=1.96.$ Then $$ \begin{array}{ll} &\left(\bar{x}-z^{*}\frac{\sigma}{\sqrt{n}}, \bar{x}+z^{*}\frac{\sigma}{\sqrt{n}}\right)\\ =&\left(105.839-1.96\frac{15}{\sqrt{31}}, 105.839+1.96\frac{15}{\sqrt{31}}\right)\\ =&(100.559,111.119) \end{array} $$
To calculate our $99\%$ confidence interval, we use $z^{*}=2.576.$ Then $$ \begin{array}{ll} &\left(\bar{x}-z^{*}\frac{\sigma}{\sqrt{n}}, \bar{x}+z^{*}\frac{\sigma}{\sqrt{n}}\right)\\ =&\left(105.839-2.576\frac{15}{\sqrt{31}}, 105.839+2.576\frac{15}{\sqrt{31}}\right)\\ =&(98.899,112.779) \end{array} $$
To calculate our $90\%$ confidence interval, we use $z^{*}=1.645.$ Then $$ \begin{array}{ll} &\left(\bar{x}-z^{*}\frac{\sigma}{\sqrt{n}}, \bar{x}+z^{*}\frac{\sigma}{\sqrt{n}}\right)\\ =&\left(105.839-1.645\frac{15}{\sqrt{31}}, 105.839+1.645\frac{15}{\sqrt{31}}\right)\\ =&(101.407,110.271) \end{array} $$
To calculate our $95\%$ confidence interval, we use $z^{*}=1.96.$ Then $$ \begin{array}{ll} &\left(\bar{x}-z^{*}\frac{\sigma}{\sqrt{n}}, \bar{x}+z^{*}\frac{\sigma}{\sqrt{n}}\right)\\ =&\left(105.839-1.96\frac{15}{\sqrt{31}}, 105.839+1.96\frac{15}{\sqrt{31}}\right)\\ =&(100.559,111.119) \end{array} $$
To calculate our $99\%$ confidence interval, we use $z^{*}=2.576.$ Then $$ \begin{array}{ll} &\left(\bar{x}-z^{*}\frac{\sigma}{\sqrt{n}}, \bar{x}+z^{*}\frac{\sigma}{\sqrt{n}}\right)\\ =&\left(105.839-2.576\frac{15}{\sqrt{31}}, 105.839+2.576\frac{15}{\sqrt{31}}\right)\\ =&(98.899,112.779) \end{array} $$