Roll the Die!Clear Everything

Distribution of Die-Roll Averages

Sample Size: $n=$ Go! Clear Everything



























The Central Limit Theorem

Draw an SRS of size $n$ from any population with mean $\mu$ and standard deviation $\sigma.$ The central limit theorem says that when $n$ (the sample size) is large, the sampling distribution of the sample means $\bar{x}$ is approximately normal with distribution with mean $\mu$ and standard deviation $\displaystyle \frac{\sigma}{\sqrt{n}}.$

That is, $$\bar{x} \sim N\left(\mu,\frac{\sigma}{\sqrt{n}}\right).$$





























So, for our fair die with $\mu=3.5$ and $\sigma=1.708,$ our "average-of-$10$-rolls" distribution is approximately $$\bar{x}\sim N\left(3.5,\frac{1.708}{\sqrt{10}}\right)=N(3.5,0.54)$$
































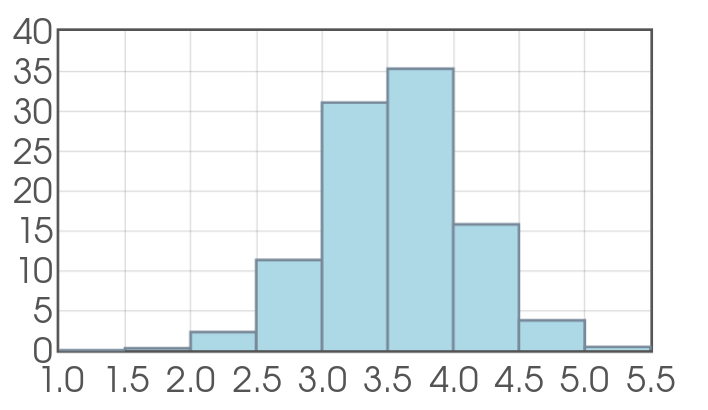
Question

For $10$ rolls, what is the approximate probability of observing a sample average of $2.5$ or less. That is, what is $P(\bar{x}\leq 2.5)?$

See The Answer!




























An Experiment

Let's suppose the average lifespan of a car battery is $\mu=4$ years.

Life spans of batteries are known to follow an exponential distribution which is very skewed.

We are going to collect data from this population.




















































The (Paraphrased) Central Limit Theorem: For any distribution, as the sample size goes up:

1) Histograms of sample averages start to look more and more normal.

2) Sample means become more tightly clustered around the true population mean.

1































Example: A geyser in Jellystone National Park named "Old Fateful" goes off at regular intervals.

The time between consecutive eruptions $X$ is uniformly distributed between $47$ and $122$ minutes.

Suppose we take a random sample of $n=72$ times between eruptions.

What is the approximate probability that the sample mean $\overline{x}$ will be between $86.377$ minutes and $88.311$ minutes?

See The Answer!































Another Example: Sleazy P. Martini Goes On Trial

Sleazy P. Martini is up to his old tricks again, throwing dice on the wharf and winning lots of bets. You (an observer with statistical knowledge) suspect that Sleazy P. is pulling some shenanigans. That is, you suspect the die he is using is loaded.

You start writing down the result of each roll of Sleazy P.'s die, and record the following data:

5 1 6 5 5 6 4 5 4 3 4 3 5 6 2 3 2 4 6 2 6 6 2 6 6 2 2 2 4 2 6 5 5 2 2 4 6 6 3 6 1 4 3 3 3 4 6 4 3 2 6 6 6 6 3 4 3 5 1 6 6 5 2 5 2 1 3 1 6 3 4 3 5 6 3 6 6 5 6 4 3 4 1 3 6 4 2 6 5 3 2 6 2 5 5 5 5 5 1 4

























Sleazy P. Martini Goes On Trial

The sample mean of the above data is $\overline{x}=4.02.$

Assuming the die is fair, what is the probability of seeing a sample mean that is $4.02$ or greater?

Is this probability in any way suggestive? See The Answer!





























In Summary

To calculate the probability that $\bar{x}$ lands in a particular interval you must first pin down three numbers:

• the sample size, $n$
• the standard deviation of the original distribution, $\sigma$
• the mean of the original distribution: $\mu$

From the above we know that $\bar{x}$ has approximately the normal distribution $\displaystyle N\left(\mu,\frac{\sigma}{\sqrt{n}}\right).$

The above following enables us to compute the following probabilities using Table A:

"$\bar{x}$ less than $\color{red}{a}$"		"$\bar{x}$ greater than $\color{red}{a}$"		"$\bar{x}$ between $\color{red}{a}$ and $\color{blue}{b}$"
$ \begin{array}{l} P(\bar{x} \leq \color{red}{a})\\ = P\left(z \leq \frac{\color{red}{a}-\mu}{\sigma/\sqrt{n}}\right)\\ = \mbox{Table A}\left(\frac{\color{red}{a}-\mu}{\sigma/\sqrt{n}}\right)\\ \end{array} $		$ \begin{array}{l} P(\bar{x} \geq \color{red}{a})\\ = P\left(z \geq \frac{\color{red}{a}-\mu}{\sigma/\sqrt{n}}\right)\\ = 1-\mbox{Table A}\left(\frac{\color{red}{a}-\mu}{\sigma/\sqrt{n}}\right)\\ \end{array} $		$ \begin{array}{l} P(a \leq \bar{x} \leq b)\\ =P\left(\frac{\color{red}{a}-\mu}{\sigma/\sqrt{n}} \leq z \leq \frac{\color{blue}{b}-\mu}{\sigma/\sqrt{n}}\right)\\ = \mbox{Table A}\left(\frac{\color{blue}{b}-\mu}{\sigma/\sqrt{n}}\right)-\mbox{Table A}\left(\frac{\color{red}{a}-\mu}{\sigma/\sqrt{n}}\right)\\ \end{array} $