Section 5.2 Lecture

Section 5.2: The Uniform Distribution Worksheet 5.2

Aww... It's your first continuous probability distribution!

Example

Suppose we arrive at a train station and all we know is that a train arrives every $8$ minutes.

What possible waiting times are there?

How is the random variable "waiting time," $X$ distributed?

A Uniform Distribution

Example: Compute the probability that a random person arriving at the station will wait less than $6.8$ minutes.

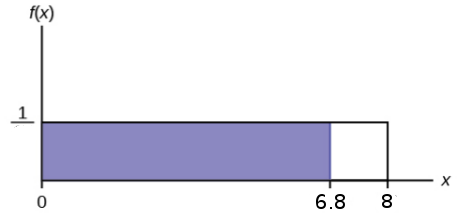
Remember: $\mbox{Probability}=\mbox{Area Under Curve}$

The height of the curve is $\displaystyle \frac{1}{8}.$

The area under the curve is then $\displaystyle\mbox{Base}\cdot \mbox{Height}=6.8\cdot \frac{1}{8}=0.85$

So, $P(X \lt 6.8)=0.85.$

A Uniform Distribution

Waiting times $X$ have the PDF $\displaystyle f(x)=\frac{1}{8}$ on the interval $0 \leq x \leq 8.$

To say that $X$ is uniformly distributed between $0$ and $8$ we write $X \sim U(0,8).$

A Uniform Distribution

Waiting times $X$ have the PDF $\displaystyle f(x)=\frac{1}{8}$ on the interval $0 \leq x \leq 8.$

Question: What is the mean $\mu$ and standard deviation $\sigma$ of this distribution?

As you might expect, the mean is $\mu=4.$

On the other hand, the standard deviation is a little more complicated. We'll put this off until a little later.

A Uniform Distribution

Example: What is the CDF?

$$F(x)=$$

The height of the curve is $\displaystyle \frac{1}{8}.$

The area under the curve is then $\displaystyle\mbox{Base}\cdot \mbox{Height}=x\cdot \frac{1}{8}=\frac{x}{8}$

So, $\displaystyle F(x)=P(X \lt x)=\frac{x}{8}.$

A Uniform Distribution

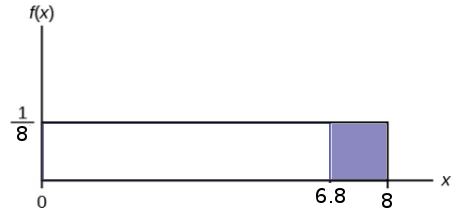
Example: Compute the probability that a random person arriving at the station will wait more than $6.8$ minutes.

Remember: $P(X \gt a)=1-F(a)$

$$ \begin{array}{lll} \displaystyle P(X \gt 6.8)&\displaystyle=1-F(6.8) &\mbox{}\\ \displaystyle &\displaystyle=1-\frac{6.8}{8} &\mbox{}\\ \displaystyle &\displaystyle=1-0.85 &\mbox{}\\ \displaystyle &\displaystyle=0.15 &\mbox{}\\ \end{array} $$

A Uniform Distribution

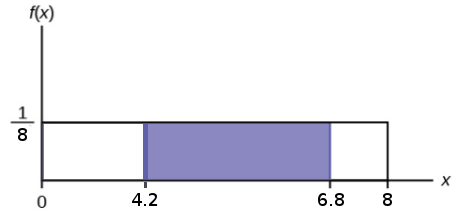
Example: Compute the probability that a random person arriving at the station will wait more than $4.2$ minutes, but less than $6.8$ minutes.

Remember: $P(a \lt X \lt b)=F(b)-F(a)$

$$ \begin{array}{lll} \displaystyle P(4.2 \lt X \lt 6.8)&\displaystyle=F(6.8)-F(4.2) &\mbox{}\\ \displaystyle &\displaystyle=\frac{6.8}{8}-\frac{4.2}{8} &\mbox{}\\ \displaystyle &\displaystyle=0.325 &\mbox{}\\ \end{array} $$

A General Uniform Distribution

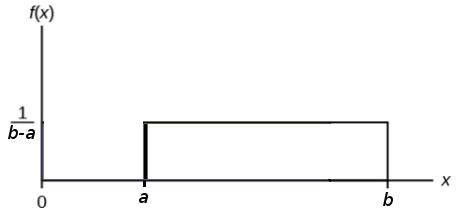
PDF: $\displaystyle f(x)=\frac{1}{b-a}$ on $a \leq x \leq b.$

A General Uniform Distribution

$\displaystyle \mu=\frac{a+b}{2} \,\,\,\,\mbox{and}\,\,\,\, \sigma=\frac{b-a}{\sqrt{12}}$

For Our Waiting-Time Distribution

$\displaystyle \mu=\frac{0+8}{2}=4 \,\,\,\,\mbox{and}\,\,\,\, \sigma=\frac{8-0}{\sqrt{12}}\approx 2.309401077$

A General Uniform Distribution

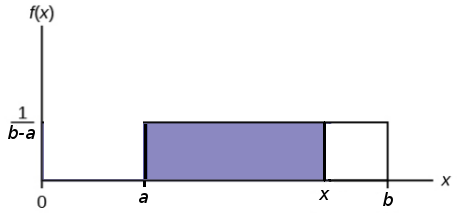
CDF: $\displaystyle F(x)=\frac{x-a}{b-a}.$

For Our Waiting-Time Distribution

CDF: $\displaystyle F(x)=\frac{x-0}{8-0}=\frac{x}{8}.$

Example

On a long, lonely stretch of straight highway in Nevada, motor vehicle accidents occur with equal probability between mile markers at $20$ miles and $42$ miles. Let $X$ be the distance as measured by the mile markers at which an accident occurs. Find $P(25 \lt X \lt 30),$ that is, the probability that the next accident will occur between mile marker $25$ and mile marker $30.$

In this example, $a=20$ and $b=42.$

To compute $P(25 \lt X \lt 30),$ we first find the CDF $F(x).$

So, $$ F(x)=\frac{x-20}{42-20}=\frac{x-20}{22} $$ We may now compute the probability. $$ \begin{array}{lll} \displaystyle P(25 \lt X \lt 30)&\displaystyle=F(30)-F(25) &\mbox{}\\ \displaystyle &\displaystyle=\frac{30-20}{22}-\frac{25-20}{22} &\mbox{}\\ \displaystyle &\displaystyle=\frac{10}{22}-\frac{5}{22} &\mbox{}\\ \displaystyle &\displaystyle=\frac{5}{22} &\mbox{}\\ \displaystyle &\displaystyle\approx 0.2272727273 &\mbox{}\\ \end{array} $$ That is, there is about a $22.7\%$ chance that the next accident will occur between mile marker $25$ and $30.$