We shall now begin a topic that is the beginning of an entire branch of applied mathematics called optimization.
The optimization problems we will be able to solve are among the many rewards we receive from our understanding of derivatives.
It is a powerful tool that that can solve really difficult problems almost like magic.
Example: Maximizing Area
Billy Bob is building a rectangular pen for his prize-winning pigs. Billy Bob has budgeted $\$330$ for fencing. One side of the pen faces the road and must be built with a more durable fencing which is $\$7$ per foot. The other three sides will be built with fencing costing $\$3$ per foot.
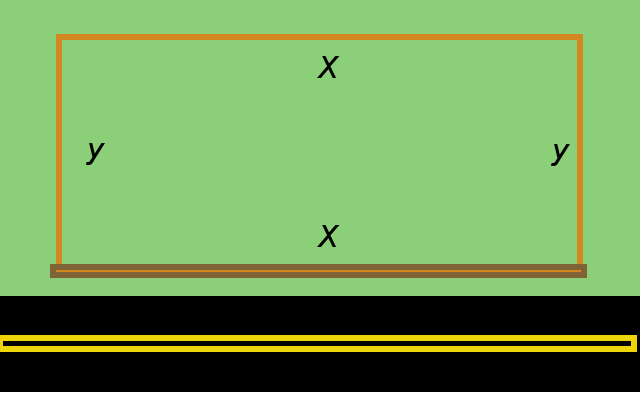
According to the figure, Billy Bob must buy $x+2y$ feet of cheap fencing.
Since the cheap fencing is $\$3$ per foot, the amount he will spend on cheap fencing is $3(x+2y)$ dollars.
Similarly, Billy Bob must buy $x$ feet of quality fencing, and since quality fencing costs $\$7$ per foot, Billy Bob will spend $7x$ dollars. Altogether, Billy Bob must spend $3(x+2y)+7x=3x+6y+7x=10x+6y$ dollars.
Since Billy Bob will be spending $\$330$ dollars, we have $10x+6y=330.$ We may simplify this equation to $5x+3y=165.$
Keeping in mind that we are trying to maximize the area of the pen, we know in general that the area of this pen will be $A=xy.$ Our cost constraint allows us to restate $x$ in terms of $y,$ or vice versa. We shall state $y$ in terms of $x:$ $$y=\frac{165-5x}{3}=55-\frac{5}{3}x$$ We may now state the area as a function of $x$ alone: $$A=xy=x\left(55-\frac{5}{3}x\right)=55x-\frac{5}{3}x^2$$ Thus, we now seek the value of $x$ which maximizes the area $A.$ We now find the critical points of the function: $$ \begin{array}{lll} & \displaystyle A'(x)=0&\\ \implies & 55-\frac{10}{3}x=0&\\ \implies & \displaystyle x=\frac{3}{10}\cdot 55&\\ \implies & \displaystyle x=16.5.&\\ \end{array} $$ Thus, $x=16.5$ is the only critical point of the function.
Since $A'(x) \gt 0$ for all $x \lt 16.5$ and $A'(x) \lt 0$ for all $x \gt 16.5,$ we know by the First Derivative Test that $x=16.5$ is an absolute maximum.
We now determine the length $y$ which yields the maximum area: $$\displaystyle y=55-\frac{5}{3}x=55-\frac{5}{3}\cdot 16.5=27.5$$ Thus, a pen which is $16.5$ feet wide and $27.5$ feet long will keep Billy Bob within his budget while maximizing the area.
Similarly, Billy Bob must buy $x$ feet of quality fencing, and since quality fencing costs $\$7$ per foot, Billy Bob will spend $7x$ dollars. Altogether, Billy Bob must spend $3(x+2y)+7x=3x+6y+7x=10x+6y$ dollars.
Since Billy Bob will be spending $\$330$ dollars, we have $10x+6y=330.$ We may simplify this equation to $5x+3y=165.$
Keeping in mind that we are trying to maximize the area of the pen, we know in general that the area of this pen will be $A=xy.$ Our cost constraint allows us to restate $x$ in terms of $y,$ or vice versa. We shall state $y$ in terms of $x:$ $$y=\frac{165-5x}{3}=55-\frac{5}{3}x$$ We may now state the area as a function of $x$ alone: $$A=xy=x\left(55-\frac{5}{3}x\right)=55x-\frac{5}{3}x^2$$ Thus, we now seek the value of $x$ which maximizes the area $A.$ We now find the critical points of the function: $$ \begin{array}{lll} & \displaystyle A'(x)=0&\\ \implies & 55-\frac{10}{3}x=0&\\ \implies & \displaystyle x=\frac{3}{10}\cdot 55&\\ \implies & \displaystyle x=16.5.&\\ \end{array} $$ Thus, $x=16.5$ is the only critical point of the function.
Since $A'(x) \gt 0$ for all $x \lt 16.5$ and $A'(x) \lt 0$ for all $x \gt 16.5,$ we know by the First Derivative Test that $x=16.5$ is an absolute maximum.
We now determine the length $y$ which yields the maximum area: $$\displaystyle y=55-\frac{5}{3}x=55-\frac{5}{3}\cdot 16.5=27.5$$ Thus, a pen which is $16.5$ feet wide and $27.5$ feet long will keep Billy Bob within his budget while maximizing the area.
Vocab
The equation involving the quantity we wish to maximize or minimize is called the objective equation.
The constraint equation describes the limits or constraints under which we are optimizing. For example, we may be operating under a limited budget, or with supply of materials.
Example: For our previous example, the objective equation is $A=xy,$ and the constraint equation is $10x+6y=330.$
General Process
- Step 1: Introduce all variables. If applicable, draw a figure and label all variables.
- Step 2: Determine which quantity is to be maximized or minimized, and for what range of values of the other variables (if this can be determined at this time).
- Step 3: Write a formula for the quantity to be maximized or minimized in terms of the variables. This formula may involve more than one variable. This is the objective equation.
- Step 4: Use the constraint equation to write the quantity to be maximized or minimized (your objective equation!) as a function of one variable.
- Step 5: Identify the domain of consideration for the function in Step 4 based on the physical problem to be solved.
- Step 6: Locate the maximum or minimum value of the function from Step 4. This step typically involves looking for critical points and evaluating a function at endpoints (if applicable).
Example: Minimizing Surface Area (i.e., Cost of Materials)
Billy Bob is designing a metal still that will have a closed cylindrical tank (the top is also covered) into which his famous Mother Lode Mountain Dew will drain. Being a skilled metal fabricator, Billy Bob will be fashioning the tank himself from an expensive form of sheet-metal suitable for commercial-grade distillation. For his purposes, Billy Bob needs to build a tank which can hold $16$ cubic feet of Mother Lode Mountain Dew.
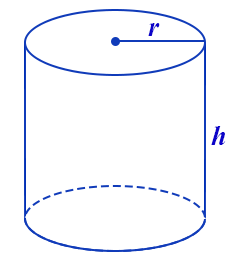
Step 1: A picture of the tank
has been provided above, and the relevant variables are the surface area $S,$ radius $r,$ and
height $h$ of the tank.
Step 2: Billy Bob wants to minimize the surface area $S$ of the tank. We know that all variables must be positive: $S \gt 0,$ $r \gt 0,$ and $h \gt 0.$
Step 3: To begin, we need to express the surface area in terms of the radius and height.
The top and bottom of the tank will be circular pieces of metal both with surface area $\pi r^2$ square feet. Then, the top and bottom of the tank require a total of $2 \pi r^2$ square feet.
The side of the tank will be a single piece of rectangular sheet metal whose width is the same as the circumference of the circular top and bottom, that is the circumference $2\pi r$ feet wide.
The height of the rectangular piece will be called $h$ so that the area of this sheet is $2\pi r h$ square feet.
The total area of the tank is then $$S=2\pi r^2+2\pi r h$$ square feet. This is the objective equation.
Step 4: The tank must have a volume of $16$ cubic feet. This is the constraint. Since the volume of a cylinder is in general $V=\pi r^2 h,$ our constraint equation is $$16=\pi r^2 h.$$
We will solve for $h$ in the constraint equation to combine with the objective equation $$h=\frac{16}{\pi r^2}.$$ Thus, $$ \begin{array}{lll} S&=2\pi r^2+2\pi r h&\\ &=\displaystyle 2\pi r^2+2\pi r\left(\frac{16}{\pi r^2}\right)&\\ &=\displaystyle 2\pi r^2+\frac{32}{r}&\\ \end{array} $$ We optimize the function expressing surface area in terms of the radius, $S(r)=2\pi r^2+\frac{32}{r}.$
Step 5: We begin by looking for critical points on the domain of consideration, $r \gt 0$ (since the radius of the cylinder must be positive).
Step 6: Finding the derivative $S'(r):$ $$ \begin{array}{lll} S'(r)&=\displaystyle \frac{d}{dr}\left(2\pi r^2+\frac{32}{r}\right)&\\ &=\displaystyle 4\pi r-\frac{32}{r^2}&\\ \end{array} $$ There aren't any critical points when $r \gt 0$ for which $S'(r)$ is undefined. Thus, we now consider points where $S'(r)=0:$ $$ \begin{array}{lll} S'(r)&=0&\\ \implies &\displaystyle 4\pi r-\frac{32}{r^2}=0&\\ \implies &\displaystyle 4\pi r^3-32=0&\mbox{ multiplying by $r^2$}\\ \implies &\displaystyle \pi r^3-8=0&\mbox{ dividing out 4}\\ \implies &\displaystyle r=\sqrt[3]{\frac{8}{\pi}}&\mbox{}\\ \implies &\displaystyle r=\frac{2}{\sqrt[3]{\pi}}&\mbox{}\\ \implies &\displaystyle r\approx 1.37&\mbox{}\\ \end{array} $$ That is, a radius of about $1.37$ feet is a candidate for a point which minimizes the surface area $S$ of the tank.
We shall use the Second Derivative Test to confirm that $\displaystyle r=\frac{2}{\sqrt[3]{\pi}}\approx 1.37$ is at least a local minimum: $$ \begin{array}{lll} S''(r)&=\displaystyle \frac{d}{dr}\left(4\pi r-\frac{32}{r^2}\right)&\\ &=\displaystyle 4\pi +\frac{64}{r^3}&\\ \end{array} $$ The expression is positive for all $r \gt 0.$ Thus, the graph of $S(r)$ is concave up over the entire domain. We conclude by the Second Derivative Test that $\displaystyle r=\frac{2}{\sqrt[3]{\pi}}\approx 1.37$ is an absolute minimum (since there are no other critical points on $r \gt 0$).
We now find the height of the tank: $$ \begin{array}{lll} h&=\displaystyle \frac{16}{\pi r^2}&\\ &=\displaystyle \frac{16}{\pi \left(\frac{2}{\sqrt[3]{\pi}}\right)^2} &\\ &=\displaystyle \frac{16}{\pi \frac{4}{\pi^{2/3}}} &\\ &=\displaystyle \frac{4}{\pi^{1/3}} &\\ &=\displaystyle \frac{4}{\sqrt[3]{\pi}} &\\ \end{array} $$ Thus, the height which minimizes the surface area is $h=\displaystyle \frac{4}{\sqrt[3]{\pi}}\approx 2.73$ feet.
In summary, the dimensions which minimize the surface of the tank are $\displaystyle r=\frac{2}{\sqrt[3]{\pi}}\approx 1.37$ feet and $h=\displaystyle \frac{4}{\sqrt[3]{\pi}}\approx 2.73$ feet.
Step 2: Billy Bob wants to minimize the surface area $S$ of the tank. We know that all variables must be positive: $S \gt 0,$ $r \gt 0,$ and $h \gt 0.$
Step 3: To begin, we need to express the surface area in terms of the radius and height.
The top and bottom of the tank will be circular pieces of metal both with surface area $\pi r^2$ square feet. Then, the top and bottom of the tank require a total of $2 \pi r^2$ square feet.
The side of the tank will be a single piece of rectangular sheet metal whose width is the same as the circumference of the circular top and bottom, that is the circumference $2\pi r$ feet wide.
The height of the rectangular piece will be called $h$ so that the area of this sheet is $2\pi r h$ square feet.
The total area of the tank is then $$S=2\pi r^2+2\pi r h$$ square feet. This is the objective equation.
Step 4: The tank must have a volume of $16$ cubic feet. This is the constraint. Since the volume of a cylinder is in general $V=\pi r^2 h,$ our constraint equation is $$16=\pi r^2 h.$$
We will solve for $h$ in the constraint equation to combine with the objective equation $$h=\frac{16}{\pi r^2}.$$ Thus, $$ \begin{array}{lll} S&=2\pi r^2+2\pi r h&\\ &=\displaystyle 2\pi r^2+2\pi r\left(\frac{16}{\pi r^2}\right)&\\ &=\displaystyle 2\pi r^2+\frac{32}{r}&\\ \end{array} $$ We optimize the function expressing surface area in terms of the radius, $S(r)=2\pi r^2+\frac{32}{r}.$
Step 5: We begin by looking for critical points on the domain of consideration, $r \gt 0$ (since the radius of the cylinder must be positive).
Step 6: Finding the derivative $S'(r):$ $$ \begin{array}{lll} S'(r)&=\displaystyle \frac{d}{dr}\left(2\pi r^2+\frac{32}{r}\right)&\\ &=\displaystyle 4\pi r-\frac{32}{r^2}&\\ \end{array} $$ There aren't any critical points when $r \gt 0$ for which $S'(r)$ is undefined. Thus, we now consider points where $S'(r)=0:$ $$ \begin{array}{lll} S'(r)&=0&\\ \implies &\displaystyle 4\pi r-\frac{32}{r^2}=0&\\ \implies &\displaystyle 4\pi r^3-32=0&\mbox{ multiplying by $r^2$}\\ \implies &\displaystyle \pi r^3-8=0&\mbox{ dividing out 4}\\ \implies &\displaystyle r=\sqrt[3]{\frac{8}{\pi}}&\mbox{}\\ \implies &\displaystyle r=\frac{2}{\sqrt[3]{\pi}}&\mbox{}\\ \implies &\displaystyle r\approx 1.37&\mbox{}\\ \end{array} $$ That is, a radius of about $1.37$ feet is a candidate for a point which minimizes the surface area $S$ of the tank.
We shall use the Second Derivative Test to confirm that $\displaystyle r=\frac{2}{\sqrt[3]{\pi}}\approx 1.37$ is at least a local minimum: $$ \begin{array}{lll} S''(r)&=\displaystyle \frac{d}{dr}\left(4\pi r-\frac{32}{r^2}\right)&\\ &=\displaystyle 4\pi +\frac{64}{r^3}&\\ \end{array} $$ The expression is positive for all $r \gt 0.$ Thus, the graph of $S(r)$ is concave up over the entire domain. We conclude by the Second Derivative Test that $\displaystyle r=\frac{2}{\sqrt[3]{\pi}}\approx 1.37$ is an absolute minimum (since there are no other critical points on $r \gt 0$).
We now find the height of the tank: $$ \begin{array}{lll} h&=\displaystyle \frac{16}{\pi r^2}&\\ &=\displaystyle \frac{16}{\pi \left(\frac{2}{\sqrt[3]{\pi}}\right)^2} &\\ &=\displaystyle \frac{16}{\pi \frac{4}{\pi^{2/3}}} &\\ &=\displaystyle \frac{4}{\pi^{1/3}} &\\ &=\displaystyle \frac{4}{\sqrt[3]{\pi}} &\\ \end{array} $$ Thus, the height which minimizes the surface area is $h=\displaystyle \frac{4}{\sqrt[3]{\pi}}\approx 2.73$ feet.
In summary, the dimensions which minimize the surface of the tank are $\displaystyle r=\frac{2}{\sqrt[3]{\pi}}\approx 1.37$ feet and $h=\displaystyle \frac{4}{\sqrt[3]{\pi}}\approx 2.73$ feet.
Example
You can run at a speed of $6$ mph and swim at a speed of $3$ mph and are located on the shore, $4$ miles east of an island that is $1$ mile north of the shoreline. How far should you run west to minimize the time needed to reach the island?
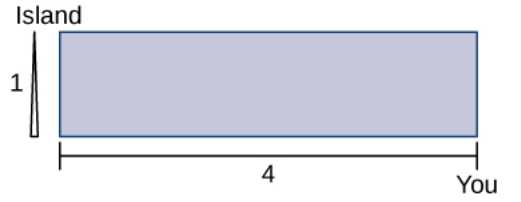
Step 1: For this problem we are interested in the time $t$ it takes to get to the island from the shore as seen in the figure.
We run $r$ miles on shore and swim $s$ miles straight to the island.
Step 2: We want to find the distance run on shore before jumping into the water that will minimize the amount of time it will take to get to the island. The amount of time will be positive: $t\gt 0,$ but will be bounded above by some slowest time.
Since the island is $4$ miles down the shore, $r$ can reasonably be any number between $0$ miles and $4$ miles, that is, $0 \leq r \leq 4.$
If we jump into the water immediately, our trip will be $\sqrt{1^2+4^2}=\sqrt{17}\approx 4.12$ miles long. That is, $s \leq \sqrt{17}.$ On the other hand, if ran the entire $4$ miles on shore, we would end up swimming $1$ mile. Thus, $1 \leq s \leq \sqrt{17}.$
Step 3: We now write an expression that will give us the total time $t$ to swim to the island. Since the rate at which we run and swim are both constant, we may use the the $\mbox{distance}=\mbox{rate}\cdot\mbox{time}$ formula. We then know that $\displaystyle \mbox{time}=\frac{\mbox{distance}}{\mbox{rate}}.$ Since we can run $6$ mph on the shore, if we run $r$ miles we get that $\displaystyle t_{\mbox{run}}=\frac{r}{6}.$ Since we can swim $3$ mph, the time when swimming is $\displaystyle t_{\mbox{swim}}=\frac{s}{3}.$ Thus, the total time getting to the island can be expressed as $$t=t_{\mbox{run}}+t_{\mbox{swim}}=\frac{r}{6}+\frac{s}{3}$$
Step 4: The constraint here is a little less obvious, but the main idea is that we want to express one quantity in terms of the other. Knowing that the swim path is the hypotenuse of a right triangle with legs $4-r$ miles (the remaining distance on shore) and $1$ mile, we can say that $s^2=(4-r)^2+1^2.$ (Let's draw this out on the figure.) Simplifying we have $s^2=r^2-8r+17.$ Thus, $$s=\sqrt{r^2-8r+17}.$$ We may now express the total time in terms of $r$ alone: $$t=\frac{r}{6}+\frac{s}{3}=\frac{r}{6}+\frac{\sqrt{r^2-8r+17}}{3}$$
Step 5: As noted already, $0 \leq r \leq 4,$ so that the domain of the problem situation is the closed an bounded interval $[0,4].$
Step 6: To minimize $t,$ we first find all critical points in $(0,4).$ Computing $t'(r):$ $$ \begin{array}{lll} t'(r)&=\displaystyle \frac{d}{dr}\left(\frac{r}{6}+\frac{\sqrt{r^2-8r+17}}{3}\right)&\\ &=\displaystyle \frac{1}{6}+\frac{1}{3}\frac{2r-8}{2\sqrt{r^2-8r+17}}&\\ &=\displaystyle \frac{1}{6}+\frac{1}{6}\frac{2r-8}{\sqrt{r^2-8r+17}}&\\ &=\displaystyle \frac{1}{6}\left(1+\frac{2r-8}{\sqrt{r^2-8r+17}}\right)&\\ \end{array} $$ We see that $t'(r)$ is undefined if $r^2-8r+17=0.$ Since the discriminant is negative, this equation has no real number solutions. Thus, there are not critical points for which $t'(r)$ is undefined.
We find critical points such that $t'(r)=0:$ $$ \begin{array}{lll} &t'(r)=0&\\ \implies &\displaystyle \frac{1}{6}\left(1+\frac{2r-8}{\sqrt{r^2-8r+17}}\right)=0&\\ \implies &\displaystyle 1+\frac{2r-8}{\sqrt{r^2-8r+17}}=0&\\ \implies &\displaystyle \frac{2r-8}{\sqrt{r^2-8r+17}}=-1&\\ \implies &\displaystyle 2r-8=-\sqrt{r^2-8r+17}&\\ \implies &\displaystyle (2r-8)^2=r^2-8r+17&\\ \implies &\displaystyle 4r^2-32r+64=r^2-8r+17&\\ \implies &\displaystyle 3r^2-24r+47=0&\\ \implies &\displaystyle r=\frac{24\pm \sqrt{12}}{6}&\\ \implies &\displaystyle r=\frac{24\pm 2\sqrt{3}}{6}&\\ \implies &\displaystyle r=\frac{12\pm \sqrt{3}}{3}&\\ \end{array} $$ The two roots are $\displaystyle r=\frac{12+ \sqrt{3}}{3} \approx 4.58$ and $\displaystyle r=\frac{12-\sqrt{3}}{3}\approx 3.42.$ Since the first root isn't in the domain of the problem situation ($[0,4]$), we discard it. Thus, $\displaystyle r=\frac{12-\sqrt{3}}{3}\approx 3.42$ is the only critical point in $[0,4].$
To determine the minimum time, we now evaluate $t(r)$ at the endpoints and critical point: $$ \begin{array}{l} \displaystyle t(0)= \frac{0}{6}+\frac{\sqrt{0^2-8\cdot 0+17}}{3}=\frac{\sqrt{17}}{3}\approx 1.37\\ \displaystyle t\left(\frac{12-\sqrt{3}}{3}\right)=\frac{\left(\frac{12-\sqrt{3}}{3}\right)}{6}-\frac{\sqrt{\left(\frac{12-\sqrt{3}}{3}\right)^2-8\cdot \left(\frac{12-\sqrt{3}}{3}\right)+17}}{3}\approx 0.96\\ \displaystyle t(4)=\frac{4}{6}+\frac{\sqrt{4^2-8\cdot 4+17}}{3}=1\\ \end{array} $$ Thus, the time to the island is minimized by running $\displaystyle r=\frac{12-\sqrt{3}}{3}\approx 3.42$ miles before jumping into the water and swimming the rest of the way.
Step 2: We want to find the distance run on shore before jumping into the water that will minimize the amount of time it will take to get to the island. The amount of time will be positive: $t\gt 0,$ but will be bounded above by some slowest time.
Since the island is $4$ miles down the shore, $r$ can reasonably be any number between $0$ miles and $4$ miles, that is, $0 \leq r \leq 4.$
If we jump into the water immediately, our trip will be $\sqrt{1^2+4^2}=\sqrt{17}\approx 4.12$ miles long. That is, $s \leq \sqrt{17}.$ On the other hand, if ran the entire $4$ miles on shore, we would end up swimming $1$ mile. Thus, $1 \leq s \leq \sqrt{17}.$
Step 3: We now write an expression that will give us the total time $t$ to swim to the island. Since the rate at which we run and swim are both constant, we may use the the $\mbox{distance}=\mbox{rate}\cdot\mbox{time}$ formula. We then know that $\displaystyle \mbox{time}=\frac{\mbox{distance}}{\mbox{rate}}.$ Since we can run $6$ mph on the shore, if we run $r$ miles we get that $\displaystyle t_{\mbox{run}}=\frac{r}{6}.$ Since we can swim $3$ mph, the time when swimming is $\displaystyle t_{\mbox{swim}}=\frac{s}{3}.$ Thus, the total time getting to the island can be expressed as $$t=t_{\mbox{run}}+t_{\mbox{swim}}=\frac{r}{6}+\frac{s}{3}$$
Step 4: The constraint here is a little less obvious, but the main idea is that we want to express one quantity in terms of the other. Knowing that the swim path is the hypotenuse of a right triangle with legs $4-r$ miles (the remaining distance on shore) and $1$ mile, we can say that $s^2=(4-r)^2+1^2.$ (Let's draw this out on the figure.) Simplifying we have $s^2=r^2-8r+17.$ Thus, $$s=\sqrt{r^2-8r+17}.$$ We may now express the total time in terms of $r$ alone: $$t=\frac{r}{6}+\frac{s}{3}=\frac{r}{6}+\frac{\sqrt{r^2-8r+17}}{3}$$
Step 5: As noted already, $0 \leq r \leq 4,$ so that the domain of the problem situation is the closed an bounded interval $[0,4].$
Step 6: To minimize $t,$ we first find all critical points in $(0,4).$ Computing $t'(r):$ $$ \begin{array}{lll} t'(r)&=\displaystyle \frac{d}{dr}\left(\frac{r}{6}+\frac{\sqrt{r^2-8r+17}}{3}\right)&\\ &=\displaystyle \frac{1}{6}+\frac{1}{3}\frac{2r-8}{2\sqrt{r^2-8r+17}}&\\ &=\displaystyle \frac{1}{6}+\frac{1}{6}\frac{2r-8}{\sqrt{r^2-8r+17}}&\\ &=\displaystyle \frac{1}{6}\left(1+\frac{2r-8}{\sqrt{r^2-8r+17}}\right)&\\ \end{array} $$ We see that $t'(r)$ is undefined if $r^2-8r+17=0.$ Since the discriminant is negative, this equation has no real number solutions. Thus, there are not critical points for which $t'(r)$ is undefined.
We find critical points such that $t'(r)=0:$ $$ \begin{array}{lll} &t'(r)=0&\\ \implies &\displaystyle \frac{1}{6}\left(1+\frac{2r-8}{\sqrt{r^2-8r+17}}\right)=0&\\ \implies &\displaystyle 1+\frac{2r-8}{\sqrt{r^2-8r+17}}=0&\\ \implies &\displaystyle \frac{2r-8}{\sqrt{r^2-8r+17}}=-1&\\ \implies &\displaystyle 2r-8=-\sqrt{r^2-8r+17}&\\ \implies &\displaystyle (2r-8)^2=r^2-8r+17&\\ \implies &\displaystyle 4r^2-32r+64=r^2-8r+17&\\ \implies &\displaystyle 3r^2-24r+47=0&\\ \implies &\displaystyle r=\frac{24\pm \sqrt{12}}{6}&\\ \implies &\displaystyle r=\frac{24\pm 2\sqrt{3}}{6}&\\ \implies &\displaystyle r=\frac{12\pm \sqrt{3}}{3}&\\ \end{array} $$ The two roots are $\displaystyle r=\frac{12+ \sqrt{3}}{3} \approx 4.58$ and $\displaystyle r=\frac{12-\sqrt{3}}{3}\approx 3.42.$ Since the first root isn't in the domain of the problem situation ($[0,4]$), we discard it. Thus, $\displaystyle r=\frac{12-\sqrt{3}}{3}\approx 3.42$ is the only critical point in $[0,4].$
To determine the minimum time, we now evaluate $t(r)$ at the endpoints and critical point: $$ \begin{array}{l} \displaystyle t(0)= \frac{0}{6}+\frac{\sqrt{0^2-8\cdot 0+17}}{3}=\frac{\sqrt{17}}{3}\approx 1.37\\ \displaystyle t\left(\frac{12-\sqrt{3}}{3}\right)=\frac{\left(\frac{12-\sqrt{3}}{3}\right)}{6}-\frac{\sqrt{\left(\frac{12-\sqrt{3}}{3}\right)^2-8\cdot \left(\frac{12-\sqrt{3}}{3}\right)+17}}{3}\approx 0.96\\ \displaystyle t(4)=\frac{4}{6}+\frac{\sqrt{4^2-8\cdot 4+17}}{3}=1\\ \end{array} $$ Thus, the time to the island is minimized by running $\displaystyle r=\frac{12-\sqrt{3}}{3}\approx 3.42$ miles before jumping into the water and swimming the rest of the way.
Example
Find the volume of the largest right circular cylinder that fits in a sphere of radius $1.$
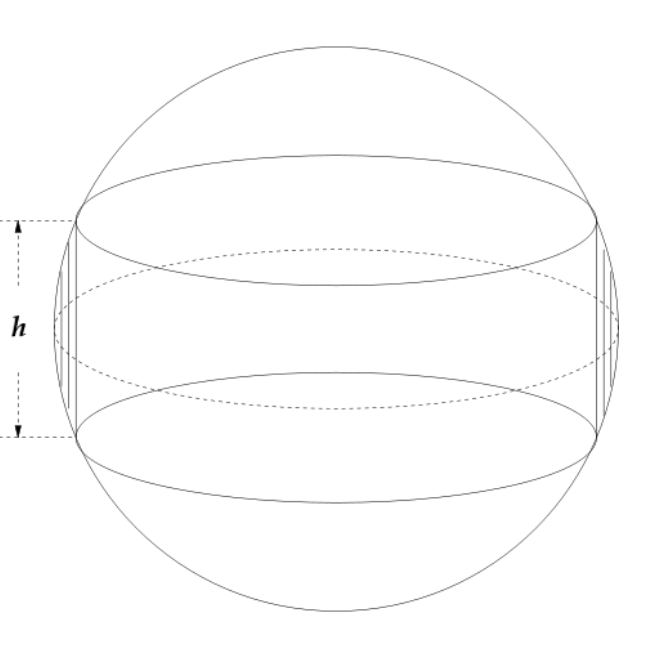
Step 1: A picture of the problem situation
has been provided above, and the relevant variables are the volume $V,$ radius $r,$ and
height $h$ of the cylinder.
Step 2: We want to maximize the volume $V$ of the cylinder. We know that all variables must be positive: $V \gt 0,$ $r \gt 0,$ and $h \gt 0.$ Since the cylinder is contained in the sphere, the radius of the cylinder cannot exceed $1$ and the height cannot exceed $2.$ Also, the volume is bounded above by an as yet unknown quantity; this is the max we want to find! However, we can say that the volume of the cylinder cannot exceed the volume of the sphere. Thus, $\displaystyle V \lt \frac{4}{3}\pi.$
Summarizing the above: $0 \lt r \lt 1,$ $0 \lt h \lt 2,$ and $\displaystyle 0 \lt V \lt \frac{4}{3}\pi.$
Step 3: The objective equation is the formula for the volume of the cylinder $\displaystyle V=\pi r^2 h$
Step 4: We shall find the constraint equation by using that the cylinder is inscribed in the sphere. Here, a figure will help us to understand the situation:
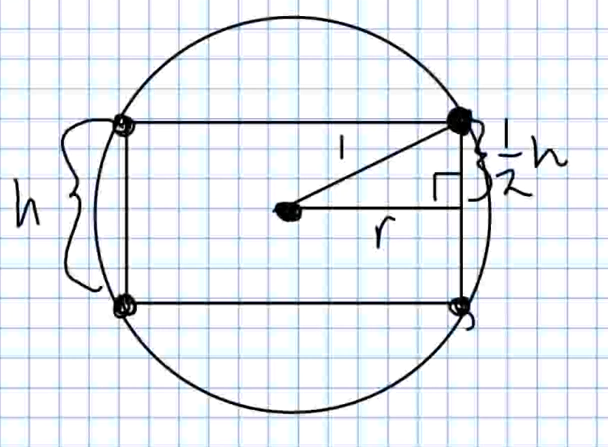
The Pythagorean Theorem give us the constraint equation on $r$ and $h:$ $\displaystyle r^2+\left(\frac{1}{2}h\right)^2=1^2,$ or more simply, $$\displaystyle r^2+\frac{1}{4}h^2=1$$ Solving the above for $r^2,$ $$r^2=1-\frac{1}{4}h^2,$$ we may now rewrite $\displaystyle V=\pi r^2 h$ as $$\displaystyle V=\pi \left(1-\frac{1}{4}h^2\right) h$$ Thus, $$V(h)=\pi \left(h-\frac{1}{4}h^3\right)$$
Step 5: The domain of the problem situation is the constraint obtained above in Step 2: $0 \lt h \lt 2.$
Step 6: To invoke the Theorem which allows us to identify absolute maxima an minima on a closed an bounded interval, we will consider $h$ on the closed and bounded interval $[0,2].$ We first consider all the critical points for $0 \lt h \lt 2.$ Now, $\displaystyle V'(h)=\pi \left(1-\frac{3}{4}h^2\right).$ There are no values for which $V'(h)$ is undefined, so we now consider points where $V'(h)=0:$ $$ \begin{array}{lll} &V'(h)=0&\\ \implies &\displaystyle \pi \left(1-\frac{3}{4}h^2\right)=0&\\ \implies &\displaystyle 1-\frac{3}{4}h^2=0&\\ \implies &\displaystyle h^2=\frac{4}{3}&\\ \implies &\displaystyle h=\pm\sqrt{\frac{4}{3}}&\\ \implies &\displaystyle h=\pm\frac{2}{\sqrt{3}}&\\ \end{array} $$ Discarding the negative root (since it is not in the domain of the problem situation), we have that $\displaystyle h=\frac{2}{\sqrt{3}}\approx 1.15$ is the only critical point on $[0,2].$ Thus our candidates for our maximum are the endpoints $0$ and $2,$ and the critical point named above. Evaluating $V(h)$ at these values we have $$ \begin{array}{l} \displaystyle V(0)=\pi \left(0-\frac{1}{4}\cdot 0^3\right)=0\\ \displaystyle V\left(\frac{2}{\sqrt{3}}\right)=\pi \left(\frac{2}{\sqrt{3}}-\frac{1}{4}\cdot \left(\frac{2}{\sqrt{3}}\right)^3\right)=\pi \left(\frac{2}{\sqrt{3}}-\frac{1}{4}\cdot \frac{8}{3\sqrt{3}}\right)=\pi \left(\frac{6}{3\sqrt{3}}-\frac{2}{3\sqrt{3}}\right)=\frac{4\pi}{3\sqrt{3}}\approx 2.42\\ \displaystyle V(2)=\pi \left(2-\frac{1}{4}\cdot 2^3\right)=0 \end{array} $$ Thus, the volume of the largest possible cylinder we can fit inside a sphere of radius $1$ is $\displaystyle \frac{4\pi}{3\sqrt{3}}=\frac{4\pi\sqrt{3}}{9}\approx 2.42$ cubic units.
Step 2: We want to maximize the volume $V$ of the cylinder. We know that all variables must be positive: $V \gt 0,$ $r \gt 0,$ and $h \gt 0.$ Since the cylinder is contained in the sphere, the radius of the cylinder cannot exceed $1$ and the height cannot exceed $2.$ Also, the volume is bounded above by an as yet unknown quantity; this is the max we want to find! However, we can say that the volume of the cylinder cannot exceed the volume of the sphere. Thus, $\displaystyle V \lt \frac{4}{3}\pi.$
Summarizing the above: $0 \lt r \lt 1,$ $0 \lt h \lt 2,$ and $\displaystyle 0 \lt V \lt \frac{4}{3}\pi.$
Step 3: The objective equation is the formula for the volume of the cylinder $\displaystyle V=\pi r^2 h$
Step 4: We shall find the constraint equation by using that the cylinder is inscribed in the sphere. Here, a figure will help us to understand the situation:

The Pythagorean Theorem give us the constraint equation on $r$ and $h:$ $\displaystyle r^2+\left(\frac{1}{2}h\right)^2=1^2,$ or more simply, $$\displaystyle r^2+\frac{1}{4}h^2=1$$ Solving the above for $r^2,$ $$r^2=1-\frac{1}{4}h^2,$$ we may now rewrite $\displaystyle V=\pi r^2 h$ as $$\displaystyle V=\pi \left(1-\frac{1}{4}h^2\right) h$$ Thus, $$V(h)=\pi \left(h-\frac{1}{4}h^3\right)$$
Step 5: The domain of the problem situation is the constraint obtained above in Step 2: $0 \lt h \lt 2.$
Step 6: To invoke the Theorem which allows us to identify absolute maxima an minima on a closed an bounded interval, we will consider $h$ on the closed and bounded interval $[0,2].$ We first consider all the critical points for $0 \lt h \lt 2.$ Now, $\displaystyle V'(h)=\pi \left(1-\frac{3}{4}h^2\right).$ There are no values for which $V'(h)$ is undefined, so we now consider points where $V'(h)=0:$ $$ \begin{array}{lll} &V'(h)=0&\\ \implies &\displaystyle \pi \left(1-\frac{3}{4}h^2\right)=0&\\ \implies &\displaystyle 1-\frac{3}{4}h^2=0&\\ \implies &\displaystyle h^2=\frac{4}{3}&\\ \implies &\displaystyle h=\pm\sqrt{\frac{4}{3}}&\\ \implies &\displaystyle h=\pm\frac{2}{\sqrt{3}}&\\ \end{array} $$ Discarding the negative root (since it is not in the domain of the problem situation), we have that $\displaystyle h=\frac{2}{\sqrt{3}}\approx 1.15$ is the only critical point on $[0,2].$ Thus our candidates for our maximum are the endpoints $0$ and $2,$ and the critical point named above. Evaluating $V(h)$ at these values we have $$ \begin{array}{l} \displaystyle V(0)=\pi \left(0-\frac{1}{4}\cdot 0^3\right)=0\\ \displaystyle V\left(\frac{2}{\sqrt{3}}\right)=\pi \left(\frac{2}{\sqrt{3}}-\frac{1}{4}\cdot \left(\frac{2}{\sqrt{3}}\right)^3\right)=\pi \left(\frac{2}{\sqrt{3}}-\frac{1}{4}\cdot \frac{8}{3\sqrt{3}}\right)=\pi \left(\frac{6}{3\sqrt{3}}-\frac{2}{3\sqrt{3}}\right)=\frac{4\pi}{3\sqrt{3}}\approx 2.42\\ \displaystyle V(2)=\pi \left(2-\frac{1}{4}\cdot 2^3\right)=0 \end{array} $$ Thus, the volume of the largest possible cylinder we can fit inside a sphere of radius $1$ is $\displaystyle \frac{4\pi}{3\sqrt{3}}=\frac{4\pi\sqrt{3}}{9}\approx 2.42$ cubic units.
Example
Set up the following optimization problem by finding the function that is to be maximized or minimized. You do not need to find the maximum or minimum value.
Suppose you are a consultant for an import gift shop that designs products to be manufactured over seas which are then shipped back to the U.S. and finally sold in their chain of shops. The company wants you to design a fancy rectangular gift box with a square base, as seen below, that has a capacity $250$ cubic inches. The materials for the lid cost $8$ cents per square inch, and the materials for the rest cost $5$ cents per square inch.
Find the dimensions of the box which minimize the cost of manufacture.
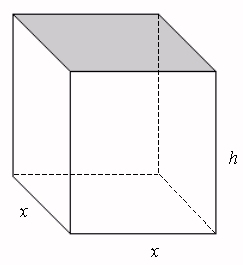
Step 1: Using the above figure, the variables are the cost $C$ of manufacture, the length of the square base $x,$ and the height $h$ of the box.
Since volume is constrained, we will call the volume of the box $V.$
Step 2: We want to minimize the cost of the box. All variables are are positive: $C \gt 0,$ $x \gt 0,$ and $h \gt 0.$
Step 3: We now write a formula which expresses the cost of materials $C$ in terms of $x$ and $h.$
Beginning with the lid, the area is $x^2,$ and since lid uses material which costs $8$ cents per square inch to manufacture, the cost for the lid is $8x^2.$
The rest of the box is composed of four side $x$-by-$h$ panels of area $xh$ plus the bottom the same area as the lid $x^2.$ The total area is then $xh+xh+xh+xh+x^2,$ or $4xh+x^2.$ Since the material used costs $5$ cents per square inch, the total cost to manufacture the rest of the box is $5(4xh+x^2),$ or $20xh+5x^2.$
The total cost to manufacture the box is $\mbox{lid}+\mbox{bottom}=8x^2+20xh+5x^2.$ That is, $$C=13x^2+20xh.$$ Step 4: We now use the constraint to write $C$ in terms of a single variable. We know that volume must be $250$ cubic inches. Since the volume of the box is $\mbox{length}\cdot\mbox{width}\cdot\mbox{height},$ or $x\cdot x \cdot h =x^2 h,$ we have $$x^2h=250.$$ We may now write the cost function in terms of a single variable. Since solving for $h$ is simplest, we'll say that $\displaystyle h=\frac{250}{x^2}$ so that $$ \begin{array}{lll} &C=13x^2+20xh&\\ \implies &\displaystyle C=13x^2+20x\left(\frac{250}{x^2}\right)& \mbox{ since $h=\frac{250}{x^2}$ by our constraint}\\ \implies &\displaystyle C=13x^2+\frac{5000}{x}& \mbox{}\\ \end{array} $$ Thus, the function to minimize is $$C(x)=13x^2+\frac{5000}{x}$$
Step 2: We want to minimize the cost of the box. All variables are are positive: $C \gt 0,$ $x \gt 0,$ and $h \gt 0.$
Step 3: We now write a formula which expresses the cost of materials $C$ in terms of $x$ and $h.$
Beginning with the lid, the area is $x^2,$ and since lid uses material which costs $8$ cents per square inch to manufacture, the cost for the lid is $8x^2.$
The rest of the box is composed of four side $x$-by-$h$ panels of area $xh$ plus the bottom the same area as the lid $x^2.$ The total area is then $xh+xh+xh+xh+x^2,$ or $4xh+x^2.$ Since the material used costs $5$ cents per square inch, the total cost to manufacture the rest of the box is $5(4xh+x^2),$ or $20xh+5x^2.$
The total cost to manufacture the box is $\mbox{lid}+\mbox{bottom}=8x^2+20xh+5x^2.$ That is, $$C=13x^2+20xh.$$ Step 4: We now use the constraint to write $C$ in terms of a single variable. We know that volume must be $250$ cubic inches. Since the volume of the box is $\mbox{length}\cdot\mbox{width}\cdot\mbox{height},$ or $x\cdot x \cdot h =x^2 h,$ we have $$x^2h=250.$$ We may now write the cost function in terms of a single variable. Since solving for $h$ is simplest, we'll say that $\displaystyle h=\frac{250}{x^2}$ so that $$ \begin{array}{lll} &C=13x^2+20xh&\\ \implies &\displaystyle C=13x^2+20x\left(\frac{250}{x^2}\right)& \mbox{ since $h=\frac{250}{x^2}$ by our constraint}\\ \implies &\displaystyle C=13x^2+\frac{5000}{x}& \mbox{}\\ \end{array} $$ Thus, the function to minimize is $$C(x)=13x^2+\frac{5000}{x}$$
Bonus Example: An Honest-to-Goodness Application
The relationship between the age $t$ of a stand of trees and the yield $y$ (timber volume in $\mbox{ft}^3$) of that stand is described by a "yield equation" $y=Y(t).$ The yield at age $t$ divided by the age $t$ is called the Mean Annual Increment $M$ and measures the rate of growth for the stand: $\displaystyle M=\frac{Y(t)}{t}.$ The age at which $M$ is maximized is known as the "rotation age."
Suppose that for a particular stand, the yield per tree is modelled by $$Y(t)=\frac{630t^2}{3t^2+8800}.$$ Find the age at which the mean annual increment $M$ is maximized, that is, find the rotation age.
This is a really nice example because the function to maximize has essentially been handed to us.
However, in practice, would would derive a function either through known models (sigmoidal growth models) or a statistical model obtained from data. For now, let's just enjoy unleashing the power of calculus!
As stated above, to obtain mean annual increment function we divide the yield $Y$ by the time $t:$ $$\displaystyle M(t)=\frac{Y(t)}{t}$$ which becomes $$M(t)=\frac{630t}{3t^2+8800}$$ This is the function we seek to maximize. Since time can be any conceivable length before harvesting, the domain the problem situation is $[0,\infty).$
We begin by looking at critical points. First, we find $M'(t):$ $$ \begin{array}{lll} M'(t)&=\displaystyle \frac{d}{dt}\frac{630t}{3t^2+8800}&\\ &=\displaystyle \frac{(3t^2+8800)(630t)'-(630t)(3t^2+8800)'}{(3t^2+8800)^2}&\\ &=\displaystyle \frac{(3t^2+8800)630-(630t)(6t)}{(3t^2+8800)^2}&\\ &=\displaystyle \frac{1890t^2+5544000-3780t^2}{(3t^2+8800)^2}&\\ &=\displaystyle \frac{5544000-1890t^2}{(3t^2+8800)^2}&\\ \end{array} $$ Since the denominator is never $0,$ the derivative is defined for all $t$ on $[0,\infty).$ Thus, we only need to find points such that $M'(t)=0:$ $$ \begin{array}{lll} &M'(t)=0&\\ \implies &\displaystyle \frac{5544000-1890t^2}{(3t^2+8800)^2}=0&\\ \implies &\displaystyle 5544000-1890t^2=0&\\ \implies &\displaystyle t^2=\frac{5544000}{1890}&\\ \implies &\displaystyle t=\sqrt{\frac{5544000}{1890}}& \mbox{ taking only the positive root since $t \in [0,\infty)$}\\ \implies &\displaystyle t\approx 54.16& \mbox{}\\ \end{array} $$ Thus, the maximum growth rate, or rotation age, of this stand is about $54.16$ years.
However, in practice, would would derive a function either through known models (sigmoidal growth models) or a statistical model obtained from data. For now, let's just enjoy unleashing the power of calculus!
As stated above, to obtain mean annual increment function we divide the yield $Y$ by the time $t:$ $$\displaystyle M(t)=\frac{Y(t)}{t}$$ which becomes $$M(t)=\frac{630t}{3t^2+8800}$$ This is the function we seek to maximize. Since time can be any conceivable length before harvesting, the domain the problem situation is $[0,\infty).$
We begin by looking at critical points. First, we find $M'(t):$ $$ \begin{array}{lll} M'(t)&=\displaystyle \frac{d}{dt}\frac{630t}{3t^2+8800}&\\ &=\displaystyle \frac{(3t^2+8800)(630t)'-(630t)(3t^2+8800)'}{(3t^2+8800)^2}&\\ &=\displaystyle \frac{(3t^2+8800)630-(630t)(6t)}{(3t^2+8800)^2}&\\ &=\displaystyle \frac{1890t^2+5544000-3780t^2}{(3t^2+8800)^2}&\\ &=\displaystyle \frac{5544000-1890t^2}{(3t^2+8800)^2}&\\ \end{array} $$ Since the denominator is never $0,$ the derivative is defined for all $t$ on $[0,\infty).$ Thus, we only need to find points such that $M'(t)=0:$ $$ \begin{array}{lll} &M'(t)=0&\\ \implies &\displaystyle \frac{5544000-1890t^2}{(3t^2+8800)^2}=0&\\ \implies &\displaystyle 5544000-1890t^2=0&\\ \implies &\displaystyle t^2=\frac{5544000}{1890}&\\ \implies &\displaystyle t=\sqrt{\frac{5544000}{1890}}& \mbox{ taking only the positive root since $t \in [0,\infty)$}\\ \implies &\displaystyle t\approx 54.16& \mbox{}\\ \end{array} $$ Thus, the maximum growth rate, or rotation age, of this stand is about $54.16$ years.
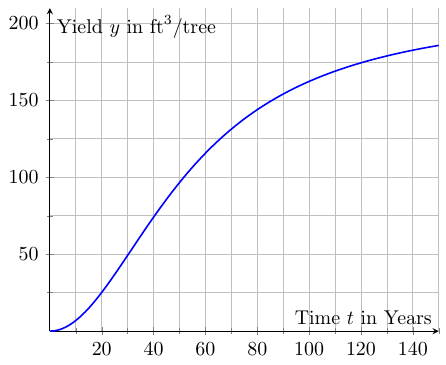 | 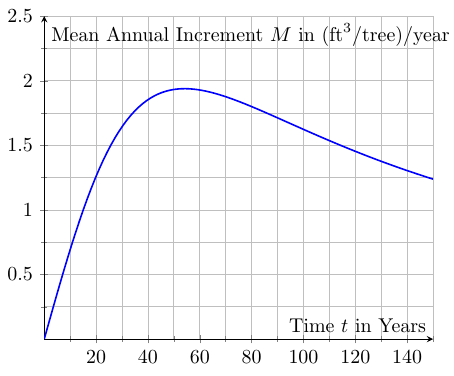 |
| $\displaystyle Y(t)=\frac{630t^2}{3t^2+8800}$ | $\displaystyle M(t)=\frac{630t}{3t^2+8800}$ |