By now, we can find derivatives of lots of functions! This is awesome!
However, what if this function walked up to you and said: "differentiate me": $$f(x)=(x^2+x+1)^{10}$$ What would you do?
Today we learn the Chain Rule which will enable us to find this derivative with the greatest of ease.
The Chain Rule
The chain rule helps us differentiate functions which are compositions with other functions.
For example, the function $h(x)=(x^2+x+1)^{10}$ is the composition of the functions $f(x)=x^{10}$ and $g(x)=x^2+x+1.$
This is because $$h(x)=(x^2+x+1)^{10}=f(x^2+x+1)=f(g(x))=(f \circ g)(x).$$ Notice there's an "outside function," $x^{10}$, and an "inside function," $x^2+x+1.$
Once we can identify "outside" and "inside" functions, we can differentiate their composition with the Chain Rule.
The Chain Rule
Let $f$ and $g$ be functions. For all $x$ in the domain of $g$ for which $g$ is differentiable at $x$ and $f$ is differentiable at $g(x),$ the derivative of the composite function $h(x)=(f\circ g)(x) =f(g(x))$ is given by $$h'(x)=f'(g(x)) \cdot g'(x).$$ We may also write $$\frac{d}{dx}[f(g(x))]=f'(g(x)) \cdot g'(x).$$ The outside function is $f$ and the inside function is $g.$
Example
$$\frac{d}{dx}(x^2+x+1)^{10}$$
The "outside function" is $x^{10}$, and the "inside function" is $x^2+x+1.$
The outside function is $f(x)=x^{10}.$ The inside function is $g(x)=x^2+x+1.$
Since $f'(x)=10x^9,$ we know that $f'(g(x))=10(x^2+x+1)^9.$
We then have $$ \begin{array}{lll} \displaystyle \frac{dy}{dx}&=\displaystyle \frac{d}{dx} f(g(x)) &\\ &=f'(g(x))\cdot g'(x) & \\ &=10(x^2+x+1)^9 (2x+1)&\\ &=10(2x+1)(x^2+x+1)^9. &\\ \end{array} $$
Since $f'(x)=10x^9,$ we know that $f'(g(x))=10(x^2+x+1)^9.$
We then have $$ \begin{array}{lll} \displaystyle \frac{dy}{dx}&=\displaystyle \frac{d}{dx} f(g(x)) &\\ &=f'(g(x))\cdot g'(x) & \\ &=10(x^2+x+1)^9 (2x+1)&\\ &=10(2x+1)(x^2+x+1)^9. &\\ \end{array} $$
Example
If $\displaystyle h(x)=\sqrt{x^3+ \frac{1}{x}},$ find $h'(x)$ and $h'(2).$
The "outside function" is _________, and the "inside function" is ____________.
The outside function is $f(x)=\sqrt{x}=x^{1/2}.$ The inside function is $g(x)=\displaystyle x^3+ \frac{1}{x}.$
Since $\displaystyle f'(x)=\frac{1}{2}x^{-1/2},$ we know that $f'(g(x))=\displaystyle \frac{1}{2}\left(x^3+ \frac{1}{x}\right)^{-1/2}.$
We then have that $$ \begin{array}{lll} \displaystyle h'(x)&=\displaystyle \frac{d}{dx} f(g(x)) &\\ &=f'(g(x))\cdot g'(x) & \\ &=\displaystyle \frac{1}{2}\left(x^3+ \frac{1}{x}\right)^{-1/2} \left(3x^2-\frac{1}{x^2}\right).&\\ \end{array} $$ So, $$ \begin{array}{lll} \displaystyle h'(2)&=\displaystyle \frac{1}{2}\left(2^3+ \frac{1}{2}\right)^{-1/2} \left(3\cdot 2^2-\frac{1}{2^2}\right) &\\ &\approx 2.015108375 & \\ \end{array} $$
Since $\displaystyle f'(x)=\frac{1}{2}x^{-1/2},$ we know that $f'(g(x))=\displaystyle \frac{1}{2}\left(x^3+ \frac{1}{x}\right)^{-1/2}.$
We then have that $$ \begin{array}{lll} \displaystyle h'(x)&=\displaystyle \frac{d}{dx} f(g(x)) &\\ &=f'(g(x))\cdot g'(x) & \\ &=\displaystyle \frac{1}{2}\left(x^3+ \frac{1}{x}\right)^{-1/2} \left(3x^2-\frac{1}{x^2}\right).&\\ \end{array} $$ So, $$ \begin{array}{lll} \displaystyle h'(2)&=\displaystyle \frac{1}{2}\left(2^3+ \frac{1}{2}\right)^{-1/2} \left(3\cdot 2^2-\frac{1}{2^2}\right) &\\ &\approx 2.015108375 & \\ \end{array} $$
Example
$$\frac{d}{dx}\frac{2}{3\sqrt{x^2+1}}$$
The "outside function" is _________, and the "inside function" is ____________.
The outside function is $\displaystyle f(x)=\frac{2}{3\sqrt{x}}=\frac{2}{3}x^{-1/2}.$ The inside function is $g(x)=\displaystyle x^2+1.$
Since $\displaystyle f'(x)=-\frac{1}{3}x^{-3/2},$ we know that $f'(g(x))=\displaystyle -\frac{1}{3}(x^2+1)^{-3/2}.$
We then have that $$ \begin{array}{lll} \displaystyle \frac{dy}{dx}&=\displaystyle \frac{d}{dx} f(g(x)) &\\ &=f'(g(x))\cdot g'(x) & \\ &=\displaystyle -\frac{1}{3}(x^2+1)^{-3/2}\cdot 2x.&\\ &=\displaystyle -\frac{2}{3}x(x^2+1)^{-3/2}.&\\ \end{array} $$
Since $\displaystyle f'(x)=-\frac{1}{3}x^{-3/2},$ we know that $f'(g(x))=\displaystyle -\frac{1}{3}(x^2+1)^{-3/2}.$
We then have that $$ \begin{array}{lll} \displaystyle \frac{dy}{dx}&=\displaystyle \frac{d}{dx} f(g(x)) &\\ &=f'(g(x))\cdot g'(x) & \\ &=\displaystyle -\frac{1}{3}(x^2+1)^{-3/2}\cdot 2x.&\\ &=\displaystyle -\frac{2}{3}x(x^2+1)^{-3/2}.&\\ \end{array} $$
Example: Chain Rule + Product Rule
$$\frac{d}{dx}\left[(2x+1)^5\sqrt{x^2+1}\right]$$
The "outside function" is _________, and the "inside function" is ____________.
$$
\begin{array}{lll}
\displaystyle \frac{dy}{dx}&=\displaystyle \frac{d}{dx} \left[(2x+1)^5\sqrt{x^2+1}\right] &\\
&= \displaystyle((2x+1)^5)'(\sqrt{x^2+1})+(2x+1)^5((x^2+1)^{1/2})'& \\
&= \displaystyle 5(2x+1)^4\cdot 2\cdot \sqrt{x^2+1}+(2x+1)^5\cdot \frac{1}{2}(x^2+1)^{-1/2}\cdot 2x& \\
&= \displaystyle 10(2x+1)^4 \sqrt{x^2+1}+x(2x+1)^5(x^2+1)^{-1/2}& \\
&= \displaystyle 10(2x+1)^4 \sqrt{x^2+1}+\frac{x(2x+1)^5}{\sqrt{x^2+1}}& \\
\end{array}
$$
The Chain Rule Redux
We can also write the chain rule in Leibniz notation. This is a fancy way to say $\frac{dy}{dx}$ notation which is sometimes called differential notation.
Let $y$ be a function of $u,$ and let $u$ be a function of $x.$
Then, $$\frac{dy}{dx}=\frac{dy}{du} \cdot \frac{du}{dx}.$$
Example
$$\frac{d}{dx}(x^2+x+1)^{10}$$
Here we can say $y=u^{10}$ (outside function) and $u=x^2+x+1$ (inside function).
Then, $$ \begin{array}{ll} \displaystyle \frac{dy}{dx}&=\displaystyle \frac{dy}{du} \cdot \frac{du}{dx}\\ &=10u^9 \cdot (2x+1) \\ &=10(x^2+x+1)^9(2x+1)\\ &=10(2x+1)(x^2+x+1)^9.\\ \end{array} $$
Example
Use the information in the following table to find $h'(a)$ at the given value for $a.$
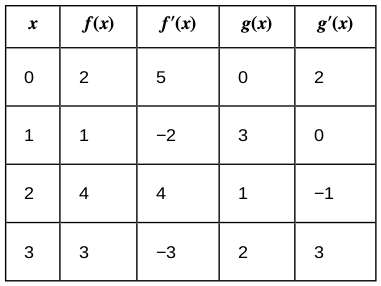
First, we find the derivative of $h(x).$
$$
\begin{array}{lll}
\displaystyle h'(x)&=\displaystyle \frac{d}{dx} \left[g \left( 2 + f ( x^2 )\right)\right] &\\
&= \displaystyle g' \left( 2 + f ( x^2 )\right)\cdot \frac{d}{dx} \left( 2 + f ( x^2 )\right) & \\
&= \displaystyle g' \left( 2 + f ( x^2 )\right)\cdot f '( x^2 )\cdot \frac{d}{dx}x^2 & \\
&= \displaystyle g' \left( 2 + f ( x^2 )\right)\cdot f '( x^2 )\cdot 2x & \\
\end{array}
$$
Then, at $a=1,$
$$
\begin{array}{lll}
\displaystyle h'(1)&=\displaystyle g' \left( 2 + f ( 1^2 )\right)\cdot f '( 1^2 )\cdot 2\cdot 1 &\\
&= \displaystyle g' \left( 2 + f ( 1 )\right)\cdot f '( 1 )\cdot 2 & \\
&= \displaystyle g' \left( 2 + 1\right)\cdot (-2)\cdot 2 & \mbox{from the table $f(1)=1, f'(1)=-2$}\\
&= \displaystyle g' \left( 3\right)\cdot (-4) & \\
&= \displaystyle 3\cdot (-4) & \mbox{from the table $g'(3)=3$}\\
&= \displaystyle -12 & \\
\end{array}
$$