The Derivative Function

The Derivative as a Function

A nice "smooth" curve like $f(x)=x^2$ has a slope (derivative) at every point $x.$

Today, we'll gather all those points and make a new function called the derivative function.

Recall: The Definition of the Derivative at a Point $a$

Let $f(x)$ be a function defined in an open interval containing $a.$ The derivative of the function $f(x)$ at $a,$ denoted by $f'(a),$ is defined to be the limit $$f'(a)=\lim_{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}$$ provided this limit exists.

Example: If $f(x)=x^2,$ then $\displaystyle f'(1) =\lim_{h \rightarrow 0} \frac{f(1+h)-f(1)}{h} =\lim_{h \rightarrow 0} \frac{(1+h)^2-1}{h} =2. $

Example: If $f(x)=x^2,$ then $\displaystyle f'(2) =\lim_{h \rightarrow 0} \frac{f(2+h)-f(2)}{h} =\lim_{h \rightarrow 0} \frac{(2+h)^2-4}{h} =4. $

The Derivative as a Function

As the above suggests, we can take any suitable value of $a$ and compute $f'(a).$

That is, we may think of the the function which takes a value $a$ as an input and hands us back $f'(a)$ as a function which we shall call $f'.$

The Derivative as a Function

$y$
	$x$

The Derivative as a Function

Let $f$ be a function. The derivative function, denoted by $f',$ is the function whose domain consists of those values of $x$ such that the following limit exists $$f'(x)=\lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}.$$

Example

Let $f(x)=2x^2+x-3.$

Use the definition of the derivative function to find $f'(x).$

The Derivative as a Function

$y$
	$x$

Example

Let $f(x)=\sqrt{x-1}.$

Use the definition of the derivative function to find $f'(x).$

$$ \begin{array}{ll} f'(x)&\\ =\displaystyle \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}&\mbox{definition of the derivative function}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\sqrt{x+h-1}-\sqrt{x-1}}{h}&\mbox{}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\sqrt{x+h-1}-\sqrt{x-1}}{h} \frac{\sqrt{x+h-1}+\sqrt{x-1}}{\sqrt{x+h-1}+\sqrt{x-1}}&\mbox{multiply by a fancy 1 with conjugates}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{(\sqrt{x+h-1}-\sqrt{x-1})(\sqrt{x+h-1}+\sqrt{x-1})}{h(\sqrt{x+h-1}+\sqrt{x-1})}&\mbox{multiply}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{x+h-1-(x-1)}{h(\sqrt{x+h-1}+\sqrt{x-1})}&\mbox{FOIL out top expression}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{x+h-1-x+1}{h(\sqrt{x+h-1}+\sqrt{x-1})}&\mbox{distribute minus}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{h}{h(\sqrt{x+h-1}+\sqrt{x-1})}&\mbox{cancel like crazy}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{1}{\sqrt{x+h-1}+\sqrt{x-1}}&\mbox{cancel $h$}\\ =\displaystyle \frac{1}{\sqrt{x-1}+\sqrt{x-1}}&\mbox{using limit results}\\ =\displaystyle \frac{1}{2\sqrt{x-1}}&\mbox{simplify}\\ \end{array} $$

The Derivative as a Function

$y$
	$x$

Sketching a Graph of a Function's Derivative

Use the graph of $y = f(x)$ to sketch the graph of its derivative $f'(x).$

Differentiability Implies Continuity

Let $f(x)$ be a function and $a$ be in its domain. If $f(x)$ is differentiable at $a,$ then $f$ is continuous at $a.$

Dire Warning

Continuity does not imply differentiability.

The function below is continuous on the interval $[-3,4],$ but is not differentiable (derivative does not exist) at $x=0$ and $x=2.$ These points are called a corners.

Dire Warning

Continuity does not imply differentiability.

The function $f(x)=\sqrt[3]{x}$ is continuous on the entire interval $(-\infty,\infty),$ but is not differentiable at $x=0$ since the tangent line is vertical.

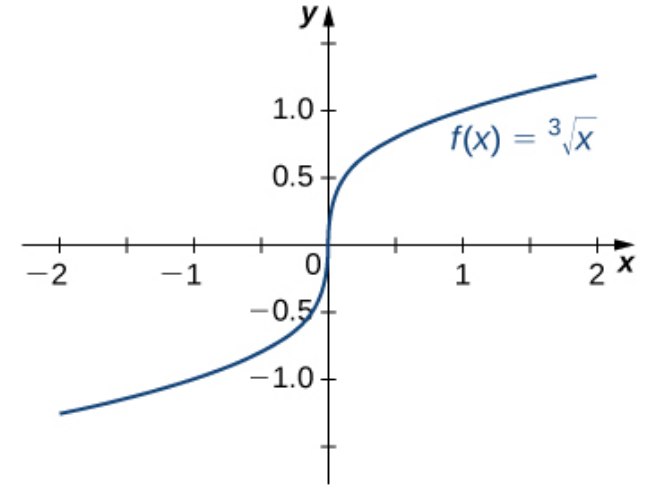
Dire Warning

Continuity does not imply differentiability.

The function $f(x)=1-\sqrt{|x-1|}$ is continuous on the entire interval $(-\infty,\infty),$ but is not differentiable at $x=1.$ This point is called a cusp.

Example

Find values of $a$ and $b$ that make the function $f(x)=\begin{cases}ax+b, & x \lt 3 \\ x^2, & x \geq 3\end{cases}$ both continuous and differentiable at $3.$

For $f(x)$ to be differentiable at $3,$ the derivatives must agree at $3.$

Since the slope of the line $y=ax+b$ is $a,$ the derivative at $3$ is $a.$ Also, the derivative of $x^2$ at $3$ is $6:$ $$ \displaystyle \lim_{h \rightarrow 0} \frac{(3+h)^2-9}{h} =\lim_{h \rightarrow 0} \frac{9+6h+h^2-9}{h} =\lim_{h \rightarrow 0} \frac{6h+h^2}{h} =\lim_{h \rightarrow 0} (6+h) =6. $$ Since the derivatives must agree, we have that $a=6.$

For $f(x)$ to be continuous at $3,$ the limit $\displaystyle \lim_{x \rightarrow 3} f(x)$ must also exist. So, the left and right-hand limits must agree. That is, $$ \begin{array}{ll} \displaystyle \lim_{x \rightarrow 3^-} f(x)=\displaystyle \lim_{x \rightarrow 3^+} f(x)&\\ \implies \displaystyle \lim_{x \rightarrow 3^-} (ax+b)=\displaystyle \lim_{x \rightarrow 3^+} x^2&\\ \implies a\cdot 3+b=9\\ \implies 6\cdot 3+b=9.& \mbox{from the above calculation}\\ \implies b=-9.& \mbox{}\\ \end{array} $$ Thus, $f(x)=\begin{cases}6x-9, & x \lt 3 \\ x^2, & x \geq 3\end{cases}$ both continuous and differentiable at $3.$

Second Derivatives

We have seen that the slope of $f(x)$ at $x$ is also a function, namely $f'(x).$ Recall that this process is called differentiation.

Fact: When we look at the slope of $f'(x),$ (i.e. differentiate again), we get a new function $f''(x)$ called the second derivative.

The second derivative $f''(x)$ is simply "the derivative of the derivative."

The Second Derivative

Let $f$ be a function and $f'$ be its derivative function. The second derivative function, denoted by $f'',$ is the function whose domain consists of those values of $x$ such that the following limit exists $$f''(x)=\lim_{h \rightarrow 0} \frac{f'(x+h)-f'(x)}{h}.$$

Example: The Second Derivative

Let $\displaystyle f(x)=\frac{1}{x}.$ Find the second derivative $f''(x).$

We first find the first derivative $f'(x):$ $$ \begin{array}{ll} f'(x)&\\ =\displaystyle \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}&\mbox{definition of the derivative function}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle\frac{1}{x+h}-\frac{1}{x}}{h}&\mbox{}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle\frac{1}{x+h}-\frac{1}{x}}{h}\frac{x(x+h)}{x(x+h)}&\mbox{multiply by fancy one to cancel denominators}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\left(\displaystyle\frac{1}{x+h}-\frac{1}{x}\right)x(x+h)}{hx(x+h)}&\mbox{multiply}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle\frac{1}{x+h}x(x+h)-\frac{1}{x}x(x+h)}{hx(x+h)}&\mbox{distribute $x(x+h)$}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle x-(x+h)}{hx(x+h)}&\mbox{cancel denominators}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle x-x-h}{hx(x+h)}&\mbox{distribute minus}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle -h}{hx(x+h)}&\mbox{cancel opposite terms}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle -1}{x(x+h)}&\mbox{cancel $h$}\\ =\displaystyle \frac{-1}{x \cdot x}&\mbox{using limit results}\\ =\displaystyle -\frac{ 1}{x^2}&\mbox{simplify}\\ \end{array} $$ Thus, $\displaystyle f'(x)=-\frac{1}{x^2}.$ We now find the second derivative $f''(x):$ $$ \begin{array}{ll} f''(x)&\\ =\displaystyle \lim_{h \rightarrow 0} \frac{f'(x+h)-f'(x)}{h}&\mbox{definition of the derivative function}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle -\frac{1}{(x+h)^2}-\left(-\frac{1}{x^2}\right)}{h}&\mbox{}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle -\frac{1}{(x+h)^2}+\frac{1}{x^2}}{h}&\mbox{simplify}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle -\frac{1}{(x+h)^2}+\frac{1}{x^2}}{h}\frac{x^2(x+h)^2}{x^2(x+h)^2}&\mbox{multiply by a fancy one to cancel denominators}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle \left(-\frac{1}{(x+h)^2}+\frac{1}{x^2}\right)x^2(x+h)^2}{hx^2(x+h)^2}&\mbox{multiply}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle -\frac{1}{(x+h)^2}x^2(x+h)^2+\frac{1}{x^2}x^2(x+h)^2}{hx^2(x+h)^2}&\mbox{distribute $x^2(x+h)^2$}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle -x^2+(x+h)^2}{hx^2(x+h)^2}&\mbox{cancel denominators}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle -x^2+x^2+2hx+h^2}{hx^2(x+h)^2}&\mbox{expand square}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle 2hx+h^2}{hx^2(x+h)^2}&\mbox{cancel opposite terms}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle h(2x+h)}{hx^2(x+h)^2}&\mbox{factor out $h$}\\ =\displaystyle \lim_{h \rightarrow 0} \frac{\displaystyle (2x+h)}{x^2(x+h)^2}&\mbox{cancel $h$}\\ =\displaystyle \frac{\displaystyle 2x}{x^2\cdot x^2}&\mbox{using limit results}\\ =\displaystyle \frac{\displaystyle 2}{x^3}&\mbox{simplify}\\ \end{array} $$ Thus, $\displaystyle f''(x)=\frac{2}{x^3}.$

Application: The Derivative as a Function

Let $P(x)$ denote the population of a city at time $x$ in years. Describe what the two expressions below represent in terms of the given situation. Be sure to include units.

a. $\,\,\,\,\displaystyle \frac{P(x+h)-P(x)}{h}$

b. $\,\,\,\,\displaystyle \lim_{h \rightarrow 0} \frac{P(x+h)-P(x)}{h}$

Other Notations for the Derivative

The function $f'(x)$ has another notation $\displaystyle \frac{dy}{dx}.$

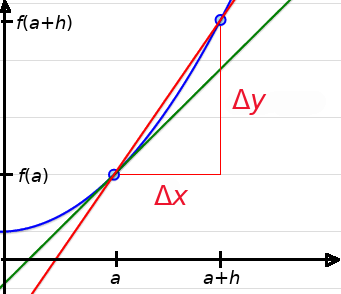
Taking $\displaystyle \frac{\Delta y}{\Delta x}= \frac{f(x+h)-f(x)}{h},$ we may write that $\displaystyle \frac{dy}{dx}=\lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}.$

Other Notations for the Derivative

Another name for $f'(x)$ is $y'.$

If $y=f(x),$ then $y'=f'(x).$

Makes sense, right?

Other Notations for the Derivative

If $y=f(x),$ then the following ALL SAY THE SAME THING:

$$y'=f'(x)$$ $$\displaystyle \frac{dy}{dx}=f'(x)$$ $$\displaystyle \frac{d}{dx}f(x)=f'(x)$$ The symbol $\displaystyle \frac{d}{dx}$ is known as the differential operator and can be read as "the derivative of."

The following are all examples of derivatives we did above but using the new $\displaystyle \frac{d}{dx}$ notation:

Example: $\displaystyle \frac{d}{dx}\frac{1}{x}=-\frac{1}{x^2}$

Example: $\displaystyle \frac{d}{dx}\sqrt{x-1}=\frac{1}{2\sqrt{x-1}}$

Example: $\displaystyle \frac{d}{dx}(2x^2+x-3)=4x+1$

Other Notations for the Second Derivative

The function $f''(x)$ has another notation $\displaystyle \frac{d^2y}{dx^2}.$

Since $f''(x)$ is the derivative of the derivative, we may write $\displaystyle \frac{d}{dx}\frac{dy}{dx}$ for which $\displaystyle \frac{d^2y}{dx^2}$ is the shorthand.

$y''$ is another notation for the second derivative since, again, if $y=f(x),$ then $y''=f''(x).$

The symbol $\displaystyle \frac{d^2}{dx^2}$ can be read as "the second derivative of."

The following is an example we did above but using the new $\displaystyle \frac{d^2}{dx^2}$ notation:

Example: $\displaystyle \frac{d^2}{dx^2}\frac{1}{x}=\frac{2}{x^3}$

Higher Order Derivatives

Third Derivative: $\displaystyle y'''=f'''(x)=\frac{d^3y}{dx^3}$

Fourth Derivative: $\displaystyle y^{(4)}=f^{(4)}(x)=\frac{d^4y}{dx^4}$

Fifth Derivative: $\displaystyle y^{(5)}=f^{(5)}(x)=\frac{d^5y}{dx^5}$

$\vdots$

$n$th Derivative: $\displaystyle y^{(n)}=f^{(n)}(x)=\frac{d^ny}{dx^n}$