Tables and graphs are a nice exploratory tool. However, they do not enable us to calculate the limit in a systematic way (such as when we solve equations or simplify expressions in algebra).
Today we learn algebraic methods for actually calculating limits.
Two Basic Results
For any real number $a$ and any constant $c$ the following limits hold: $$\lim_{x\rightarrow a} x=a$$ $$\lim_{x\rightarrow a} c=c.$$ Example: $\,\,\,\,\displaystyle \lim_{x\rightarrow 5} x=5$
Example: $\,\,\,\,\displaystyle \lim_{x\rightarrow 5} 10=10$
With these basic rules, and the limit laws we are about to introduce, we will be able to find limits for large classes of functions.
Limit Laws
Let $f(x)$ and $g(x)$ be defined for all $x \neq a$ over some open interval containing $a.$ Assume that $L$ and $M$ are real numbers such that $\displaystyle \lim_{x \rightarrow a} f(x)=L$ and $\displaystyle \lim_{x \rightarrow a} g(x)=M.$ Then the following hold:
$\displaystyle \lim_{x \rightarrow a}\left[ f(x)+g(x) \right]=\lim_{x \rightarrow a} f(x)+\lim_{x \rightarrow a} g(x)=L+M$
$\displaystyle \lim_{x \rightarrow a}\left[ f(x)-g(x) \right]=\lim_{x \rightarrow a} f(x)-\lim_{x \rightarrow a} g(x)=L-M$
$\displaystyle \lim_{x \rightarrow a}cf(x)=c\lim_{x \rightarrow a} f(x)=cL$ for any constant $c$
$\displaystyle \lim_{x \rightarrow a}\left[ f(x) \cdot g(x) \right]=\lim_{x \rightarrow a} f(x) \cdot \lim_{x \rightarrow a} g(x)=L \cdot M$
$\displaystyle \lim_{x \rightarrow a}\frac{f(x)}{g(x)}=\frac{\displaystyle\lim_{x \rightarrow a} f(x)}{\displaystyle\lim_{x \rightarrow a} g(x)}=\frac{L}{M}$ provided $M \neq 0$
Limit Laws (Continued)
Let $f(x)$ and $g(x)$ be defined for all $x \neq a$ over some open interval containing $a.$ Assume that $L$ and $M$ are real numbers such that $\displaystyle \lim_{x \rightarrow a} f(x)=L$ and $\displaystyle \lim_{x \rightarrow a} g(x)=M.$ Then the following hold:
$\displaystyle \lim_{x \rightarrow a}\left[ f(x) \right]^n=\left[\lim_{x \rightarrow a} f(x)\right]^n=L^n$ for any positive integer $n$
$\displaystyle \lim_{x \rightarrow a}\sqrt[n]{ f(x)}=\sqrt[n]{\lim_{x \rightarrow a} f(x)}=\sqrt[n]{L},$ note that $L\geq 0$ if $n$ is even
Limit Laws
Example: Use the limit laws to evaluate $\displaystyle \lim_{x \rightarrow 6}[(2x-1)\sqrt{x+4}].$ In each step, indicate the limit law applied.
$$
\begin{array}{ll}
\displaystyle \lim_{x \rightarrow 6}\left[(2x-1)\sqrt{x+4}\right] & \mbox{}\\
=\displaystyle \left( \lim_{x \rightarrow 6}(2x-1)\right) \left(\lim_{x \rightarrow 6}\sqrt{x+4}\right) & \mbox{The limit of a product is the product of the limits.}\\
=\displaystyle \left( \lim_{x \rightarrow 6}(2x)-\lim_{x \rightarrow 6} 1\right) \left(\lim_{x \rightarrow 6}\sqrt{x+4}\right) & \mbox{The limit of a difference is the difference of the limits.}\\
=\displaystyle \left( \lim_{x \rightarrow 6}(2x)-\lim_{x \rightarrow 6} 1\right) \left(\sqrt{\lim_{x \rightarrow 6}(x+4)}\right) & \mbox{The limit of a root is the root of the limit.}\\
=\displaystyle \left( \lim_{x \rightarrow 6}(2x)-\lim_{x \rightarrow 6} 1\right) \left(\sqrt{\lim_{x \rightarrow 6}x+\lim_{x \rightarrow 6} 4}\right) & \mbox{The limit of a sum is the sum of the limits.}\\
=\displaystyle \left( 2\lim_{x \rightarrow 6}x-\lim_{x \rightarrow 6} 1\right) \left(\sqrt{\lim_{x \rightarrow 6}x+\lim_{x \rightarrow 6} 4}\right) & \mbox{The limit of a multiple is the multiple of the limits.}\\
=\displaystyle \left( 2\cdot 6-1\right) \left(\sqrt{6+4}\right) & \mbox{$\displaystyle \lim_{x\rightarrow a} x=a$ and $\displaystyle \lim_{x\rightarrow a} c=c.$}\\
=11\sqrt{10}
\end{array}
$$
Limit Laws
Example: Use the following graphs of $f(x)$ an $g(x)$ and the limit laws to evaluate the limits.
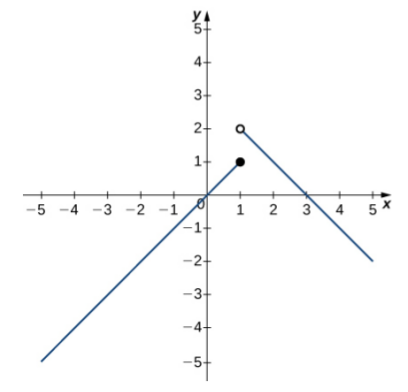 |  |
| $f(x)$ | $g(x)$ |
(a) $\,\,\,\displaystyle \lim_{x \rightarrow -1} [f(x)+g(x)]$$=\displaystyle \lim_{x \rightarrow -1}f(x)+\displaystyle \lim_{x \rightarrow -1}g(x)=-1+2=1$
(b) $\,\,\,\displaystyle \lim_{x \rightarrow 2} \frac{f(x)g(x)}{3}$ $= \frac{\displaystyle \lim_{x \rightarrow 2}f(x)\displaystyle \lim_{x \rightarrow 2}g(x)}{\displaystyle \lim_{x \rightarrow 2}3}=\displaystyle\frac{1 \cdot 0}{3}=0$
(c) $\,\,\,\displaystyle \lim_{x \rightarrow 2} \frac{2+g(x)}{f(x)}$$= \frac{\displaystyle \lim_{x \rightarrow 2}2+\displaystyle \lim_{x \rightarrow 2}g(x)}{\displaystyle \lim_{x \rightarrow 2}f(x)}=\displaystyle \frac{2+0}{1}=2$
(d) $\,\,\,\displaystyle \lim_{x \rightarrow 3} \frac{2+g(x)}{f(x)}$$\,\,\,\,\mbox{Can't use quotient law since $\displaystyle \lim_{x \rightarrow 3}f(x)=0.$}$
Limit Laws
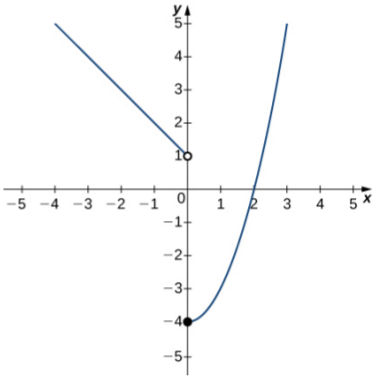
Example: Use the following graphs of $f(x)$ an $g(x)$ and the limit laws to evaluate the limits.
 |  |
| $f(x)$ | $g(x)$ |
(a) $\,\,\,\,\displaystyle \lim_{x \rightarrow 1} [f(x)-2g(x)]$
$\,\,\,\,\mbox{$\displaystyle \lim_{x \rightarrow 1} f(x)$ does not exist. Therefore, the limit does not exist. (DNE)}$
(b) $\,\,\,\,\displaystyle \lim_{x \rightarrow 1^-} [f(x)-2g(x)]$ $=\displaystyle \lim_{x \rightarrow 1^-}f(x)-2\displaystyle \lim_{x \rightarrow 1^-}g(x)= 1-2\cdot (-3)=7$
(c) $\,\,\,\,\displaystyle \lim_{x \rightarrow 1^+} [f(x)-2g(x)]$ $=\displaystyle \lim_{x \rightarrow 1^+}f(x)-2\displaystyle \lim_{x \rightarrow 1^+}g(x)= 2-2\cdot (-3)=8$
(b) $\,\,\,\,\displaystyle \lim_{x \rightarrow 1^-} [f(x)-2g(x)]$ $=\displaystyle \lim_{x \rightarrow 1^-}f(x)-2\displaystyle \lim_{x \rightarrow 1^-}g(x)= 1-2\cdot (-3)=7$
(c) $\,\,\,\,\displaystyle \lim_{x \rightarrow 1^+} [f(x)-2g(x)]$ $=\displaystyle \lim_{x \rightarrow 1^+}f(x)-2\displaystyle \lim_{x \rightarrow 1^+}g(x)= 2-2\cdot (-3)=8$
Limits of Polynomials and Rational Functions
Since limits behave very nicely with sums, differences, products, and quotients, finding limits of polynomial and (many) rational functions is a breeze:
Limit Law Corollary: For any polynomials $p(x)$ and $q(x),$ and any real number $a,$ the following hold:
$\displaystyle \lim_{x \rightarrow a} p(x)=p(a)$
$\displaystyle \lim_{x \rightarrow a} \frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}$ provided $q(a) \neq 0$
Example: $\,\,\,\,\displaystyle \lim_{x \rightarrow -2} (3x^2-2x+7)$ $=3(-2)^2-2(-2)+7=23$
Example: $\,\,\,\,\displaystyle \lim_{x \rightarrow 2} \frac{x^2-3x+2}{x^2-1}$ $=\displaystyle \frac{2^2-3\cdot 2+2}{2^2-1}=\displaystyle \frac{0}{3}=0$
Dire Warning
When calculating a limit using limit laws, we must make sure that the individual limits exist.
Although it's nice when we can, it's not always true that we can simply "plug in the value" to calculate the limit.
Sometimes the job requires a bit more finesse.
The Finer Points
Recall that we "calculated" the limit $\displaystyle \lim_{x\rightarrow 2}\frac{x^2-4}{x-2}=4$ using tables and graphs.
We will now use the limit laws to calculate this limit, but we need to do a little prep work before we do since we can't simply "plug in" $x=2$ into the expression $\displaystyle \frac{x^2-4}{x-2}.$
$$
\begin{array}{ll}
\displaystyle \lim_{x\rightarrow 2}\frac{x^2-4}{x-2} & \mbox{}\\
=\displaystyle \lim_{x\rightarrow 2}\frac{(x-2)(x+2)}{x-2} & \mbox{ Factor the numerator.}\\
=\displaystyle \lim_{x\rightarrow 2}(x+2) & \mbox{ We can cancel the factor of $x-2$ since $x$ is never equal to 2.}\\
=4 & \mbox{using sub rule for polynomials}\\
\end{array}
$$
More Finer-Point Limits
$\displaystyle \lim_{x \rightarrow 1} \frac{x^2-3x+2}{x^2-1}$
$$
\begin{array}{ll}
\displaystyle \lim_{x \rightarrow 1} \frac{x^2-3x+2}{x^2-1} & \mbox{}\\
=\displaystyle \lim_{x \rightarrow 1} \frac{(x-1)(x-2)}{(x-1)(x+1)} & \mbox{ Factor the numerator and denominator.}\\
=\displaystyle \lim_{x \rightarrow 1} \frac{x-2}{x+1}& \mbox{ We can cancel the factor of $x-1$ since $x$ is never equal to 1.}\\
=\displaystyle -\frac{1}{2} & \mbox{using sub rule for rational functions}\\
\end{array}
$$
$\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{4+x}-2}{x}$
$$
\begin{array}{ll}
\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{4+x}-2}{x} & \mbox{}\\
=\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{4+x}-2}{x}\frac{\sqrt{4+x}+2}{\sqrt{4+x}+2} & \mbox{ Rationalize the numerator.}\\
=\displaystyle \lim_{x \rightarrow 0} \frac{4+x-4}{x(\sqrt{4+x}+2)} & \mbox{ After Multiplying.}\\
=\displaystyle \lim_{x \rightarrow 0} \frac{x}{x(\sqrt{4+x}+2)} & \mbox{ After Simplifying.}\\
=\displaystyle \lim_{x \rightarrow 0} \frac{1}{\sqrt{4+x}+2} & \mbox{ We can cancel the factor of $x$ since $x$ is never equal to 0.}\\
=\displaystyle \frac{1}{4} & \mbox{ Using limit laws.}\\
\end{array}
$$
$\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{a+x}-\sqrt{a}}{x}$
$$
\begin{array}{ll}
\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{a+x}-\sqrt{a}}{x} & \mbox{}\\
=\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{a+x}-\sqrt{a}}{x}\frac{\sqrt{a+x}+\sqrt{a}}{\sqrt{a+x}+\sqrt{a}} & \mbox{ Rationalize the numerator.}\\
=\displaystyle \lim_{x \rightarrow 0} \frac{a+x-a}{x(\sqrt{a+x}+\sqrt{a})} & \mbox{ After Multiplying.}\\
=\displaystyle \lim_{x \rightarrow 0} \frac{x}{x(\sqrt{a+x}+\sqrt{a})} & \mbox{ After Simplifying.}\\
=\displaystyle \lim_{x \rightarrow 0} \frac{1}{\sqrt{a+x}+\sqrt{a}} & \mbox{ We can cancel the factor of $x$ since $x$ is never equal to 0.}\\
=\displaystyle \frac{1}{2\sqrt{a}} & \mbox{ Using limit laws.}\\
\end{array}
$$