We now begin with a truly fundamental notion which is the foundation all of calculus and many areas of advanced mathematics.
The limit of a function is the idea underpinning everything we study from here on out.
A Thought Experiment
Suppose we were to invest $\$1$ into a savings account which pays $100\%$ interest annually. After $1$ year we would have $\$2$ as seen in our table below.
| $n$ | $\displaystyle \left(1+\frac{1}{n}\right)^{n}$ |
Another Example of Limiting Behavior
| $y$ | | |
| $x$ |
Yet Another Example of Limiting Behavior
$y=x^2, \,\, 0 \leq x \leq 2$
| $y$ | $y$ | ||
| $x$ | $x$ |
The Limit of a Function
All the above is to demonstrate that understanding limiting behavior will enable us to do the mathematics we want to do.
Finding slopes of tangent lines and areas under curves are the two big problems we will tackle in MTH 241 and MTH 242. Thus, understanding limiting processes will be key to understanding the ideas we cover in this course.
We shall now begin our formal investigation of limiting processes by studying the limit of a function.
The Limit of a Function
| $y=\displaystyle \frac{x^2-4}{x-2}$ | | |
| $x$ |
The Limit of a Function
Example: Since the $y$ values of the function $\displaystyle f(x)=\frac{x^2-4}{x-2}$ get closer and closer to $4$ as $x$ gets closer and closer to $2,$ we write $$\lim_{x\rightarrow 2}\frac{x^2-4}{x-2}=4.$$
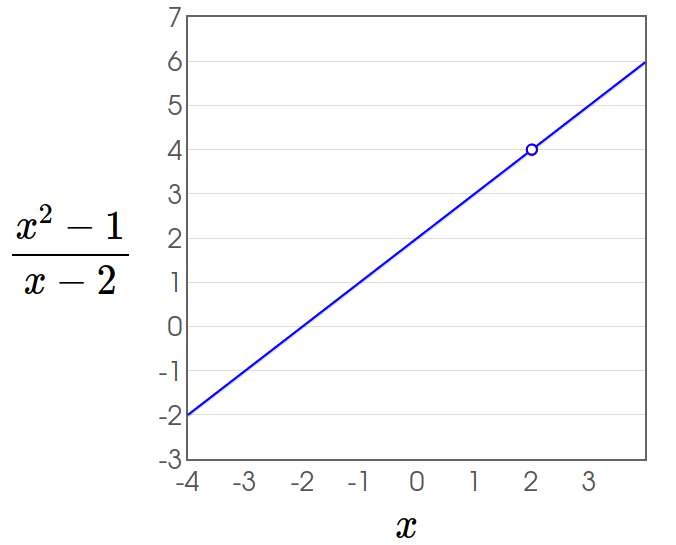
The Limit of a Function
We could have also used a table of values of $\displaystyle \frac{x^2-4}{x-2}$ as $x$ gets closer and closer to $2.$
| $x$ | $\displaystyle \frac{x^2-4}{x-2}$ |
The Intuitive Definition of a Limit
Let $f(x)$ be a function defined at all values in an open interval containing $a,$ with the possible exception of $a$ itself, and let $L$ be a real number. If all values of the function $f(x)$ approach the real number $L$ as the values of $x$ (not equal to $a$) approach the number $a,$ then we say that the limit of $f(x)$ as $x$ approaches $a$ is $L.$
Symbolically, we express this idea as $$\lim_{x \rightarrow a} f(x)=L.$$ More succinctly we may say that as $x$ gets closer to $a,$ $f(x)$ gets closer and stays close to $L.$
The Limit of a Function
Example: Estimate $\displaystyle \lim_{x \rightarrow 1} \frac{\frac{1}{x}-1}{x-1}$ using a table of functional values. Use a graph to confirm your estimate.
| $x$ | $\displaystyle \frac{\frac{1}{x}-1}{x-1}$ |
The Limit of a Function
Example (Continued): Estimate $\displaystyle \lim_{x \rightarrow 1} \frac{\frac{1}{x}-1}{x-1}$ using a table of functional values. Use a graph to confirm your estimate.
Limits Don't Always Exist
| $y=\displaystyle \frac{|x^2-4|}{x-2}$ | | |
| $x$ |
When a Limit Does Not Exist
Since the $y$ values of the function $\displaystyle f(x)=\frac{|x^2-4|}{x-2}$ do not get closer and closer to a single value as $x$ gets closer and closer to $2,$ we say that the limit $$\lim_{x\rightarrow 2}\frac{|x^2-4|}{x-2}$$ does not exist.
We may also write $\mbox{DNE}$ to say that "the limit does not exist."
One-Sided Limits: In applications it is common to restrict the domain of a function. For example, we might say that time is always greater than zero, or that distances cannot be negative. In this case, a one-sided limit may exist. For the example we considered above, both one-sided limits exist.
As $x$ approaches $2$ from the left-hand side, $\displaystyle f(x)=\frac{|x^2-4|}{x-2}$ approaches $-4.$
As $x$ approaches $2$ from the right-hand side, $\displaystyle f(x)=\frac{|x^2-4|}{x-2}$ approaches $4.$
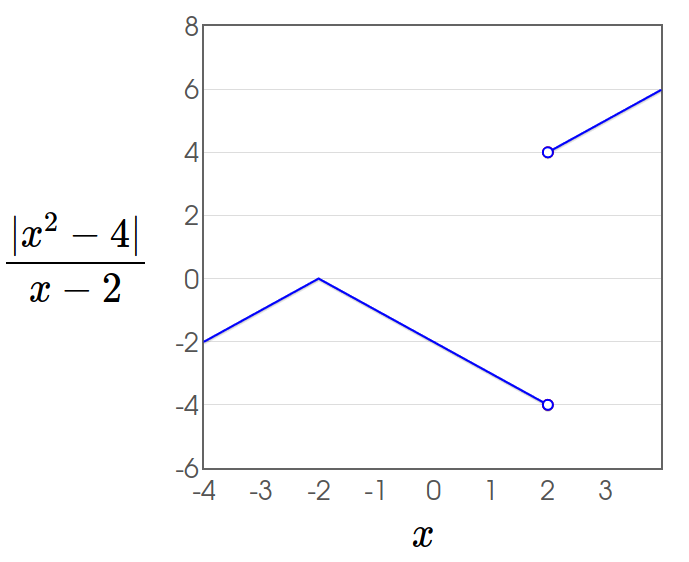
One-Sided Limits
For the left-sided limit we write $\displaystyle \lim_{x \rightarrow 2^{-}}\frac{|x^2-4|}{x-2}=-4$
For the right-sided limit we write $\displaystyle \lim_{x \rightarrow 2^{+}}\frac{|x^2-4|}{x-2}=4$

Limit from the Left
Let $f(x)$ be a function defined at all values in an open interval of the form $(c,a)$, and let $L$ be a real number. If the values of the function $f(x)$ approach the real number $L$ as the values of $x$ (where $x\lt a$) approach the number $a,$ then we say that $L$ is the limit of $f(x)$ as $x$ approaches $a$ from the left.
Symbolically, we express this idea as $$\lim_{x \rightarrow a^{-}} f(x)=L.$$ More succinctly we may say that as $x$ approaches $a$ from the left, $f(x)$ gets closer and stays close to $L.$
Limit from the Right
Let $f(x)$ be a function defined at all values in an open interval of the form $(a,c)$, and let $L$ be a real number. If the values of the function $f(x)$ approach the real number $L$ as the values of $x$ (where $x \gt a$) approach the number $a,$ then we say that $L$ is the limit of $f(x)$ as $x$ approaches $a$ from the right.
Symbolically, we express this idea as $$\lim_{x \rightarrow a^{+}} f(x)=L.$$ More succinctly we may say that as $x$ approaches $a$ from the right, $f(x)$ gets closer and stays close to $L.$
A Useful Theorem
Two-Sided limits and one-sided limits are related. Intuitively, it makes sense that if the left and right-hand limits exist, and both are the same value $L,$ then the two sided limit exists. Conversely, if the two-sided limit exists and is equal to $L,$ then the left and right-hand limits also exist and are equal to $L.$
Theorem
Let $f(x)$ be a function defined at all values in an open interval containing $a,$ with the possible exception of $a$ itself, and let $L$ be a real number. Then,
$\displaystyle \lim_{x \rightarrow a} f(x)=L$ if and only if $\displaystyle \lim_{x \rightarrow a^{+}} f(x)=L$ and $\displaystyle \lim_{x \rightarrow a^{-}} f(x)=L.$
Example
Let $f(x)=\begin{cases}x+1 \mbox{ if $x \lt 2$}\\ x^2-4 \mbox{ if $x \geq 2$}\end{cases}.$ Show that the limit $\displaystyle \lim_{x \rightarrow 2} f(x)$ does not exist.
Example
Let $f(x)=\begin{cases}x+1 \mbox{ if $x \lt 2$}\\ x^2-4 \mbox{ if $x \geq 2$}\end{cases}.$ Show that the limit $\displaystyle \lim_{x \rightarrow 2} f(x)$ does not exist.

From the graph we see that $\displaystyle \lim_{x \rightarrow 2^{-}} f(x)=3$ and $\displaystyle \lim_{x \rightarrow 2^{+}} f(x)=0.$ Since the left and right-hand limits are not equal, the two-sided limit $\displaystyle \lim_{x \rightarrow 2} f(x)$ does not exist.
Infinite Limits
Sometimes as we approach a value, the function values get either very large in the positive direction or the the negative direction.
Let's consider the behavior of the function $\displaystyle f(x)=\frac{1}{(x+1)^2}$ as $x$ approaches $-1.$
| $x$ | $\displaystyle \frac{1}{(x+1)^2}$ |
Infinite Limits
From the above we see that as $x$ approaches $-1$ from both the left and right-hand side, we can make $\displaystyle f(x)=\frac{1}{(x+1)^2}$ as large as we please.
In this case we have an infinite limit, and we may write $\displaystyle \lim_{x \rightarrow -1}\frac{1}{(x+1)^2}=\infty$
We also note that the left and right-hand limits are also infinite, that is
$\displaystyle \lim_{x \rightarrow -1^-}\frac{1}{(x+1)^2}=\infty$ and $\displaystyle \lim_{x \rightarrow -1^+}\frac{1}{(x+1)^2}=\infty$
Infinite Limits
The left and right-hand limits won't always agree as we have seen already.
Let's consider the behavior of another function $\displaystyle f(x)=\frac{1}{(x+1)^3}$ as $x$ approaches $-1.$
| $x$ | $\displaystyle \frac{1}{(x+1)^3}$ |
Infinite Limits
From the above we see that as $x$ approaches $-1$ from both the left, we can make $\displaystyle f(x)=\frac{1}{(x+1)^3}$ as large as we please in the negative direction. On the other hand, as $x$ approaches $-1$ from both the right, we can make $\displaystyle f(x)=\frac{1}{(x+1)^3}$ as large as we please in the positive direction. Thus, we may write
$\displaystyle \lim_{x \rightarrow -1^-}\frac{1}{(x+1)^3}=-\infty$ and $\displaystyle \lim_{x \rightarrow -1^+}\frac{1}{(x+1)^3}=\infty.$