Calculus: Putting the "fun" in "functions!"
Question: Can you be in two different places at once?
Answer: For gods and superheros, maybe. For the rest of us, however, our location is a function of time.
That is, at every instant of time, we can be in one and only one place.
Example: Let's draw a graph of our distance $y$ from home as function of time $x.$
A Plausible Graph
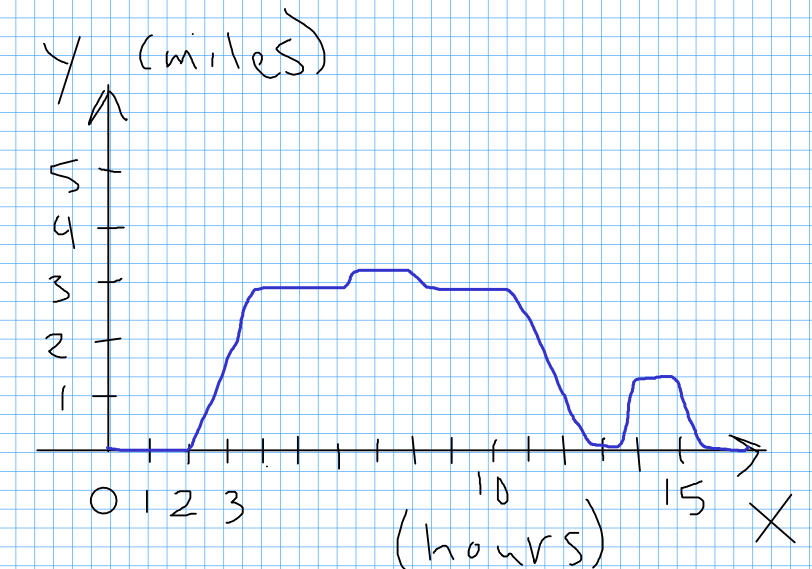
An Implausible Graph
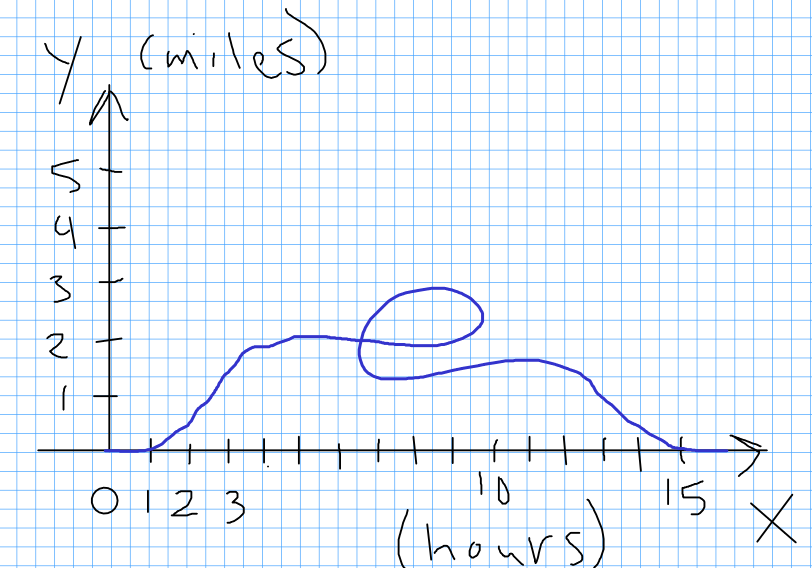
Observation: for every value on the horizontal axis, a function must have one and only one vertical component. (Otherwise, we're in two or more places at once!)
Formal Statement: The graph of a function must pass the vertical line test.
Example: Which relation below is the graph of a function?
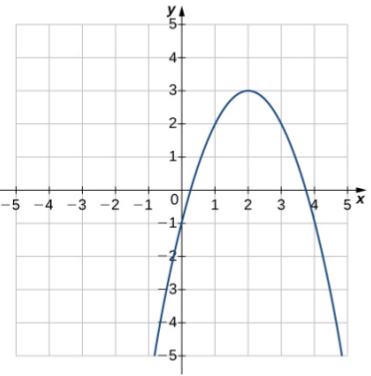
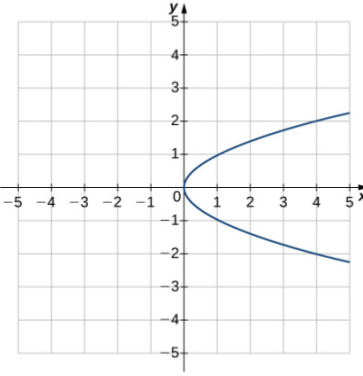
Functions as Tables

Functions as Formulas
A function can also be represented as a formula. For example, the relation $y=\sqrt{1-x},$ defines $y$ as a function of $x.$
From this formula, we can make a table of values and a graph.
| $$ \begin{array}{c|c} x & y \\ \hline -3 & \\ -2 & \\ -1 & \\ 0 & \\ 1 & \\ 2 & \\ 3 & \\ \end{array} $$ |
|
Domain and Range of a Function
As we saw in the previous example, not all $x$-values agree well with a function. All of the values of $x$ which don't give a function a belly ache is called the domain of a function.
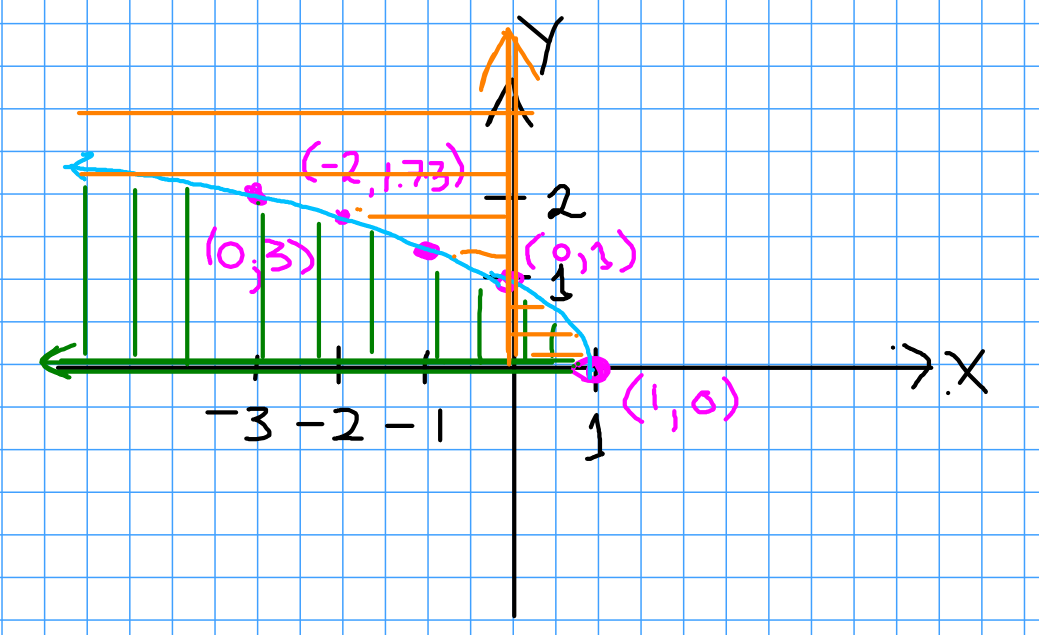
Example: Find the domain $D_f$ and the range $R_f$ of the function $f(x)=\sqrt{1-x}.$
$\displaystyle D_f=(-\infty, 1],$ $R_f=[0,\infty)$

Other Important Features of a Function
$x$-Intercepts and $y$-Intercept
Values of $x$ for which $f(x)$ is increasing/decreasing.
Example: Find the $x$ and $y$ intercepts and intervals where $f$ is increasing and decreasing for the function $$f(x)=\sqrt{1-x}.$$
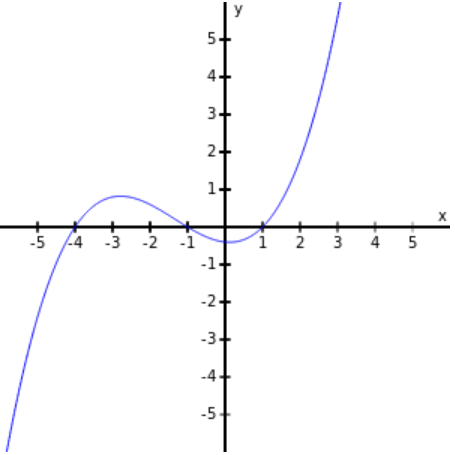
Important Features of Functions and Their Graphs
 | 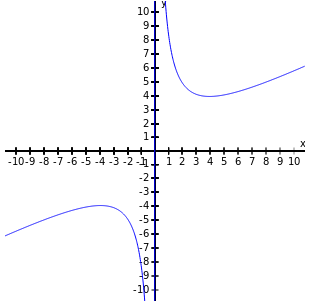 | 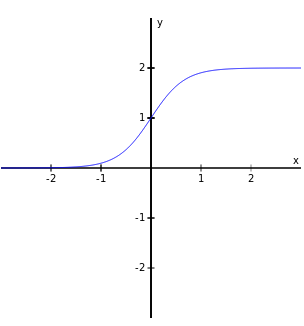 | |
| Domain | $(-\infty,\infty)$ | $(\infty,0) \cup (0,\infty)$ | $(-\infty,\infty)$ |
| Range | $(-\infty,\infty)$ | $(\infty,-4] \cup [4,\infty)$ | $(0,1)$ |
| $x$-intercepts | $x=-4,$ $-1,$ and $1$ | none | none |
| $y$-intercept | $y\approx -0.4$ | none | $y=1$ |
| Increasing | $(\infty,-3) \cup (0,\infty)$ | $(\infty,-4) \cup (4,\infty)$ | $(-\infty,\infty)$ |
| Decreasing | $(-3,0)$ | $(-4,0) \cup (0,4)$ | $\varnothing$ |
| Symmetry | none | odd | about $y$ axis |
Arithmetic Operations on Functions
Definition: Let $f$ and $g$ be functions on the same domain $D.$ Then:
We define the function $f+g$ by $(f+g)(x)=f(x)+g(x).$
We define the function $f-g$ by $(f-g)(x)=f(x)-g(x).$
We define the function $f \cdot g$ by $(f \cdot g)(x)=f(x) \cdot g(x).$
We define the function $\displaystyle \frac{f}{g}$ by $\displaystyle\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}.$
Domain
The domains of $f+g,$ $f-g,$ and $f \cdot g$ are all equal to $\{x|x \in D_f \mbox{ and } x \in D_g\}.$
The domain of $\displaystyle \frac{f}{g}$ is $\{x|x \in D_f \mbox{ and } x \in D_g \mbox { and } g(x)\neq 0 \}.$
Arithmetic Operations on Functions
Example: Consider the functions $\displaystyle f(x)=\frac{1}{x-2}$ and $\displaystyle g(x)=\frac{1}{x-1}.$
a. Find $f+g$, $f-g,$ $f \cdot g$ and simplify your answers completely.
$\displaystyle(f+g)(x)=f(x)+g(x)=\frac{1}{x-2}+\frac{1}{x-1}=\frac{2x-3}{(x-2)(x-1)}$
$\displaystyle (f-g)(x)=f(x)-g(x)=\frac{1}{x-2}-\frac{1}{x-1}=\frac{1}{(x-2)(x-1)}$
$\displaystyle(f \cdot g)(x)=f(x) \cdot g(x)=\frac{1}{x-2}\cdot\frac{1}{x-1}=\frac{1}{(x-2)(x-1)}$
b. Find the the domain of $f+g,$ $f-g,$ and $f \cdot g.$
$$D_{f+g}=D_{f-g}=D_{f \cdot g}=\{x|x \in D_f \mbox{ and } x \in D_g\}=(-\infty,1)\cup (1,2)\cup(2,\infty)$$
c. Find $\displaystyle \frac{f}{g}$ and simplify your answer completely.
$\displaystyle \left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}=\frac{\displaystyle\frac{1}{x-2}}{\displaystyle\frac{1}{x-1}}=\frac{x-1}{x-2}$
d. Find the the domain of $\displaystyle \frac{f}{g}.$
 $$D_{\frac{f}{g}}=\{x|x \in D_f \mbox{ and } x \in D_g \mbox { and } g(x)\neq 0 \}=(-\infty,1)\cup (1,2)\cup(2,\infty)$$
$$D_{\frac{f}{g}}=\{x|x \in D_f \mbox{ and } x \in D_g \mbox { and } g(x)\neq 0 \}=(-\infty,1)\cup (1,2)\cup(2,\infty)$$
Another Operation on Functions: Composition.
Suppose $g$ sends $-2$ to $3$, and $f$ sends $3$ to $5.$ That is, in symbols $g(-2)=3$, and $f(3)=5.$
If we daisy-chain these two functions together, we get the composition: $$f(g(-2))=f(3)=5.$$ The above we may write more simply as $$(f \circ g)(-2)=5.$$
Compositions of Functions
A function composition is a function of a function.
Definition: Let $g$ be a function with domain $A$ and range $B$, and let $f$ be a function with domain $B$ and range $C.$
Then the composition of $f$ and $g$, denoted $f \circ g$, is defined to be $$(f \circ g)(x)=f(g(x)).$$
Example: Consider the functions $f(x)=\sqrt{1-x^2}$ and $\displaystyle g(x)=\sqrt{x}.$
Find $(f \circ g)(x)$ and $(g \circ f)(x).$
$$ \begin{array}{ll} (f \circ g)(x)&=f(g(x))\\ &=f(\sqrt{x})=\sqrt{1-(\sqrt{x})^2}\\ &=\sqrt{1-x} \end{array} $$
$$ \begin{array}{ll} (g \circ f)(x)&=g(f(x))\\ &=g(\sqrt{1-x^2})\\ &=\sqrt{\sqrt{1-x^2}}\\ &=\sqrt[4]{1-x^2} \end{array} $$
Domain of Function Compositions
The domain of $f \circ g$ is given by $D_{f \circ g}=\{x|x \in D_g \mbox{ and } g(x) \in D_f\}.$
The domain of $g \circ f$ is given by $D_{g \circ f}=\{x|x \in D_f \mbox{ and } f(x) \in D_g\}.$
Example: Consider the functions $f(x)=\sqrt{1-x^2}$ and $\displaystyle g(x)=\sqrt{x}.$
Find the domains $D_{f \circ g}$ and $D_{g \circ f}.$

$$ \begin{array}{ll} D_{f \circ g}&=\{x|x \in D_g \mbox{ and } g(x) \in D_f\}\\ &=\{x|x \in [0,\infty) \mbox{ and } \sqrt{x} \in [-1,1]\}\\ &=\{x|x \geq 0 \mbox{ and } -1 \leq \sqrt{x} \leq 1\}\\ &=\{x|x \geq 0 \mbox{ and } 0\leq x \leq 1\}\\ &=[0,1] \end{array} $$ $$ \begin{array}{ll} D_{g \circ f}&=\{x|x \in D_f \mbox{ and } f(x) \in D_g\}\\ &=\{x|x \in [-1,1] \mbox{ and } \sqrt{1-x^2} \in [0,\infty)\}\\ &=\{x| -1 \leq x \leq 1 \mbox{ and } \sqrt{1-x^2} \geq 0 \} \\ &=\{x| -1 \leq x \leq 1 \mbox{ and } 1-x^2 \geq 0\}\\ &=\{x| -1 \leq x \leq 1 \mbox{ and } x^2 \leq 1 \}\\ &=[-1,1] \end{array} $$
Application
Example: A certain bacterium grows in culture in a circular region.
The radius of the circle, measured in centimeters, is given by $\displaystyle r(t) = 6 - \frac{5}{t^2+1},$ where $t$ is time measured in hours since a circle of a $1$-cm radius of the bacterium was put into the culture.
a. Express the area of the bacteria as a function of time.
The area of a circle is given by $A=\pi r^2.$ Thus, $$ \begin{array}{ll} A(t)&=\pi (r(t))^2\\ &=\pi\left(6 - \frac{5}{t^2+1}\right)^2.\\ \end{array} $$ b. Find the exact and approximate area of the bacterial culture in $3$ hours.
$$ \begin{array}{ll} A(3)&=\pi (r(3))^2\\ &=\pi\left(6 - \frac{5}{3^2+1}\right)^2\\ &=\pi\left(6 - \frac{5}{10}\right)^2\\ &=\pi\left(6 - \frac{1}{2}\right)^2\\ &=\pi\left(\frac{11}{2}\right)^2\\ &=\frac{121\pi}{4}\\ &\approx 95.03 \end{array} $$ That is, the area of the culture is approximately $95.03 \mbox{ cm}^2.$