Definition: a set is a well-defined collection of objects.
By "well-defined," we mean that we can objectively decide whether or not an object belongs to a collection.
Example
Consider the collection or set $F$ of all current SWOCC faculty. We may write $$\mbox{Mr. Holt} \in F.$$ The above says that "Mr. Holt is an element of $F.$"
On the other hand, John Lennon is not a member of the current SWOCC faculty. Thus, $$\mbox{John Lennon} \notin F.$$ The above says that "John Lennon is not an element of $F.$"
Example of a Collection Which is NOT Well-Defined
Let $M$ be the collection of all musical acts which are "awesooooome!"
$M$ is not a set because the collection is not well-defined. For example, I might say $\mbox{Led Zeppelin}\in M,$ whereas a young whipper-snapper in this class might disagree with me and say $\mbox{Led Zeppelin}\notin M.$
Since there is no objective way to pin down the elements of $M,$ it is not a well-defined collection, and is therefore not a set.
Example
Consider the set of months of the year $L$ which have $31$ days. $$L=\{\mbox{January},\mbox{March},\mbox{May},\mbox{July},\mbox{August},\mbox{October},\mbox{December}\}$$ Note that $\mbox{March} \in L,$ but $\mbox{April} \notin L$
The above illustrates $2$ methods of writing sets. The phrase "the set of all months the year which have $31$ days" illustrates the descriptive method.
On the other hand, listing all the elements of a set between braces, i.e., "$\{$" and "$\}$," is called the roster method.
Set Builder Notation
Another notation we will use to write sets is called set-builder notation. For the sets we've discussed so far, $$P=\{x|\mbox{$x$ is a person in this room at this moment}\}$$ $$L=\{x|\mbox{$x$ is a month with 31 days}\}$$
Infinite Sets
The set of natural numbers $N$ is the collection of all counting numbers $\{1,2,3,4,\ldots\}$
The set of odd natural numbers $O$ is the collection $\{1,3,5,7,\ldots\}$
The set of even natural numbers $E$ is the collection $\{2,4,6,8,\ldots\}$
The set of integers $Z$ is the collection $\{\ldots,-4,-3,-2,-1,0,1,2,3,4,\ldots\}$
Example: All three notations below are valid ways of writing the set of all integers between $-5$ and $5.$
Descriptive: The set of all integers between $-5$ and $5.$
Roster: $\{-4,-3,-2,-1,0,1,2,3,4\}$
Set-Builder: $\{x| x \in Z \mbox{ and } -5 \lt x \lt 5 \}$
Pop Quiz!
How many elements does the set $\{x| x \in O \mbox{ and } 0 \lt x \lt 10 \}$ have?
How many elements does the set $\{x| \mbox{ $x$ is a member of the Beatles who has attended SWOCC} \}$ have?
The Empty Set
Yes, it turns out that the set $$\{x| \mbox{ $x$ is a member of the Beatles who has attended SWOCC} \}$$ doesn't have any elements.
This is OKAY! In fact this set is a very important set called the empty set and has a special notation: $\varnothing.$
For sets, $\varnothing$ plays a similar role $0$ does for the integers.
The Empty Set
Another notation for the empty set is just a pair of braces $\{\}$.
So $$\varnothing=\{\}$$
Cardinality
The number of distinct elements of a set $A$ is called its cardinality and is denoted $n(A).$
Note: $n(A)$ is also called the the cardinal number of $A.$
Examples: Cardinality
$n(\{2,3,5,7\})=4$
Let $A=\{x| x \in O \mbox{ and } 0 \lt x \lt 10 \}.$ Then $n(A)=5.$
$n(\{-4,-3,-2,-1,0,1,2,3,4\})=9$
Trickier Examples: Cardinality
$n(\varnothing)=0$
$n(\{\varnothing\})=1$
$n(\{2178\})=1$
$n(N)$ is not a any number that we we know since the set of natural numbers $N$ is an infinite set.
Set Equality
Two sets $A$ and $B$ are said to be equal if they have the same elements.
Example: Let $A=\{1,2,3\}$ and $B=\{2,1,3\}$. Then $A$ and $B$ ARE EQUAL since both sets have the same elements.
Example: If $A=\{1,2,3\}$ and $B=\{1,2,4\}$, then $A$ and $B$ are NOT equal since they do not have the same elements..
Set Equality
Technical Note: We also note that we may list set elements twice, but they still count as one distinct element.
For example, $\{1,2,3\}=\{1,2,2,3\}$
However, we will stick with the convention of listing distinct elements only once.
A Universal Set
When we study a particular set of objects, for example the natural numbers, we have a universal set which is the entire scope of our consideration.
Definition: The universal set $U$ is the collection of all the objects we wish to study in a particular situation.
In algebra, very often the universal set is either all real numbers $R$ or the complex numbers $C.$
The Complement of a Set
Now that we have some notion of what our universe consists of, we can now define an important idea that will present itself later in the course.
Definition: The complement of the set $A$, denoted $A',$ is the collection of all elements not in $A.$ We may write $$A'=\{x| x \in U \mbox{ and } x\notin A\}$$
Venn Diagrams
If we imagine sets as containers with things in them, we can visualize sets using the notion of a Venn Diagram as seen below.
Venn Diagrams tell us what elements are in a set, and what elements ARE NOT in a set.
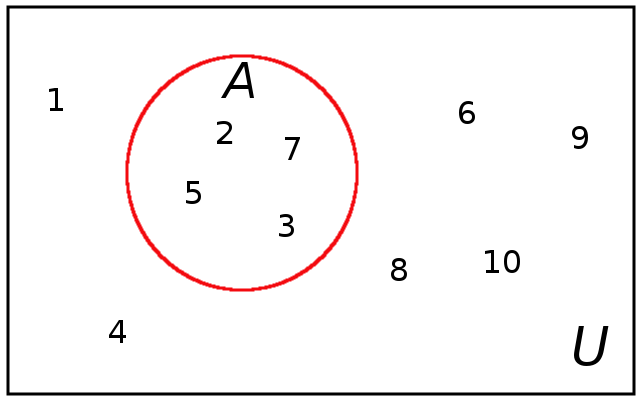
Venn Diagrams
For example, below we see that $2,$ $3,$ $5,$ and $7$ are in the set $A,$ but that $1,$ $4,$ $6,$ and $8$, $9,$ and $10$ ARE NOT in $A.$

We also plainly see that $U=\{1,2,3,4,5,6,7,8,9,10\}$, $A=\{2,3,5,7\},$ and $A'=\{1,4,6,8,9,10\}$
Subsets
Most sets contain smaller sets within them. For example our set $A=\{2,3,5,7\}$ from above contains the set $C=\{3,7\}$ because every element of $C$ is also an element of $A.$
The same can be said of $D=\{2,3,5\}.$
Both sets $C$ and $D$ are called subsets of $A$ since they are contained entirely within $A.$
In both of these cases we write $C \subseteq A$ and $D \subseteq A.$
Subsets
Definition: If every element of a set $A$ is also in $B,$ we say that $A$ is a subset of $B$ and we write $A \subseteq B.$
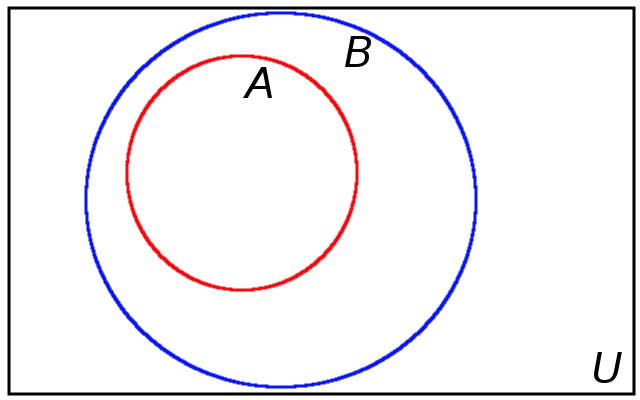
We also say that "$A$ is contained in $B.$"
Example
List all the subsets of $A=\{\natural, 1, \diamondsuit\}.$
Fact
Every set is a subsets of itself. For example, $$\{\natural, 1, \diamondsuit\}\subseteq \{\natural, 1, \diamondsuit\}.$$ That is, for any set $A,$ we can say $A \subseteq A$
This motivates another definition...
Definition: Suppose $A \subseteq B,$ but $A \neq B.$ Then $A$ is called a proper subset of $B$.
If $A$ is a proper subset of $B,$ we may (if we like) write $A \subset B.$
Example: $\{1, \diamondsuit\}$ is a proper subset of $\{\natural, 1, \diamondsuit\}.$ Therefore, we may write $\{1, \diamondsuit\} \subset \{\natural, 1, \diamondsuit\}$
Fun Fact
The number of possible subsets of a set $A$ is $2^{n(A)}.$
Example: We saw that there were a total of $2^{n(A)}=2^3=8$ subsets of $A=\{\natural, 1, \diamondsuit\}.$
Question: What is the number of proper subsets?
Set Operations
We can put numbers together to get new numbers by performing operations such as addition and multiplication.
For example, if we take the numbers $2$ and $3$, we can combine them to get other numbers: $2+3$ gives us $5,$ and $2 \cdot 3$ gives us $6.$
Sets also have operations we can perform on them to get new sets.
We now look at several examples of combining old sets to make new sets.
The Union of Two Sets
When we take the elements from two sets $A$ and $B$ and put them into a single set, we form their union and write $A \cup B.$
Example: In the above, $A \cup B=\{1,2,3,4,5,6,7,8,9\}.$
The Union of Two Sets
Definition: Let $A$ and $B$ be sets. We define the union of $A$ and $B$ to be the set $$A \cup B=\{x| x \in A \mbox{ or } x \in B\}.$$
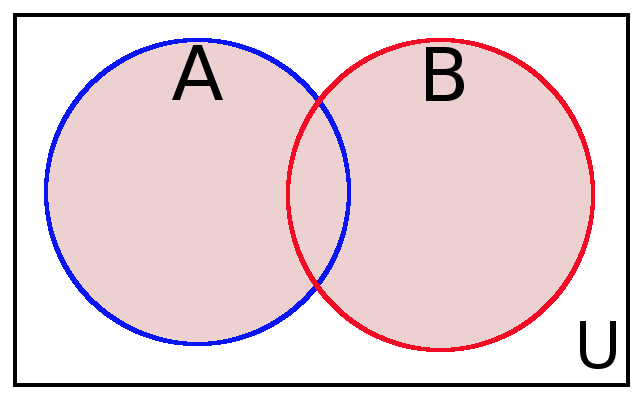
The union is shaded pink in the above Venn diagram.
Example
Let $X=\{\heartsuit,w,3,4\}$ and $Y=\{5,4,\clubsuit\}.$
Find $X \cup Y.$
The Intersection of Two Sets
When we take the collection of elements which simultaneously belong to two sets $A$ and $B$, we form their intersection and write $A \cap B.$

Example: In the above, $A \cap B=\{6\}.$
The Intersection of Two Sets
Definition: Let $A$ and $B$ be sets. We define the intersection of $A$ and $B$ to be the set $$A \cap B=\{x| x \in A \mbox{ and } x \in B\}.$$
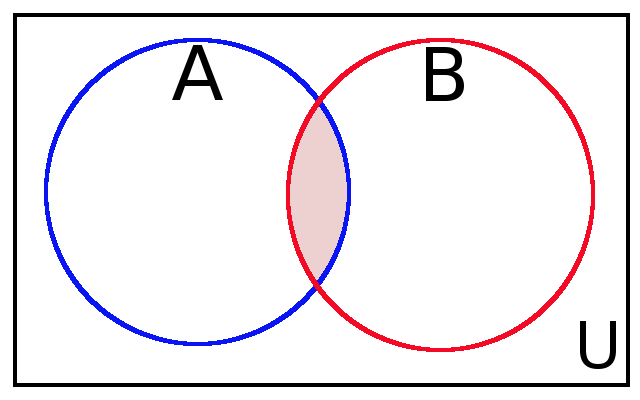
The intersection is shaded pink in the above Venn diagram.
Example: Let $X=\{\heartsuit,8,\flat,\blacktriangle,\clubsuit\}$ and $Y=\{8,\blacktriangle,9,\clubsuit,z\}.$
Find $X \cap Y.$
Example: Let $A=\{\blacktriangle,\natural\}$ and $B=\{r,\flat,a,\bigstar,2,z\}$
Find $A \cap B$
Combining Union, Intersection, and Complement
Example: Let the universal set be $U=\{1,2,3,4,5,6,7,8\}.$ Define sets $A,$ $B,$ and $C$ as follows:
$A=\{2,3,5,7\}$
$B=\{1,4\}$
$C=\{2,4,6,8\}$
Find $(A \cup B)' \cap C.$
The Cardinality of Unions
Let $A$ and $B$ be sets. Then the cardinality of their union $A \cup B$ is given by the following: $$n(A \cup B)=n(A)+n(B)-n(A \cap B)$$
The Cardinality of Unions
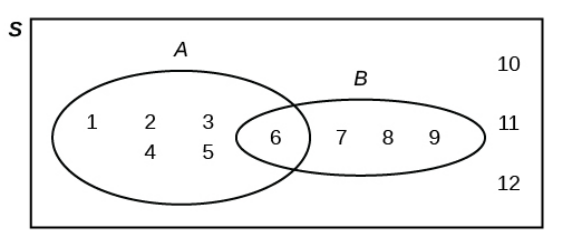
Example: Verify that $n(A \cup B)=n(A)+n(B)-n(A \cap B)$ by using the figure below.

The Cardinality of Unions
Example: Suppose $n(A)=7,$ $n(B)=5,$ and $n(A \cap B)=3.$
Find $n(A \cup B).$