Cryptography: A Less-Than-Complete Introduction in Five Acts
Benjamin V. Holt
Southwestern STEM Colloquium
November 8th, 2019
Benjamin V. Holt
Southwestern STEM Colloquium
November 8th, 2019
Cryptography is an ancient and modern practice.





Act I
A Whirlwind Tour of Modular Arithmetic
A Whirlwind Tour of Modular Arithmetic
Modular Arithmetic
Modular arithmetic is remainder arithmetic.
Two numbers are "equal" if they have the same remainder when dividing by a fixed number called the modulus.
For example, $19$ and $10$ have the same remainder when we divide both by $9.$
We may write the above as $19 \equiv 10 \equiv 1 \,\,(\mbox{mod } 9).$

Modular Arithmetic
If you can answer the following question, then you are already familiar with one example of modular arithmetic:
It's 11 am. What time will it be in 4 hours?
Modular Arithmetic
Yes! Colloquium time!
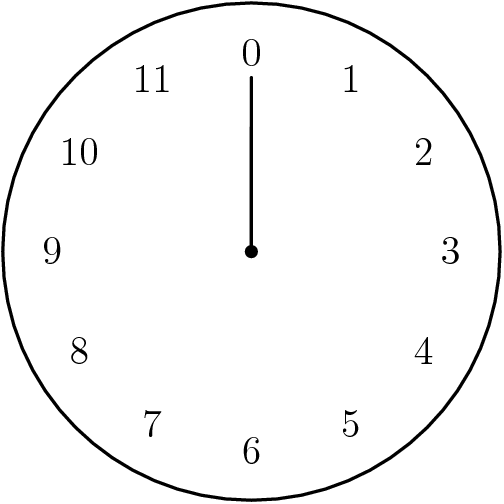

We just performed arithmetic modulo $12$: $$11+4 \equiv 15 \equiv 3 \,\,(\mbox{mod } 12).$$
Modular Arithmetic

Modular Arithmetic: Examples.
| $9+7 \equiv \,\,\,\,(\mbox{mod } 12)$ | $9 \cdot 7 \equiv \,\,\,\,(\mbox{mod } 12)$ |  |
| $8+3 \equiv \,\,\,\,(\mbox{mod } 9)$ | $8 \cdot 3 \equiv \,\,\,\,(\mbox{mod } 9)$ | 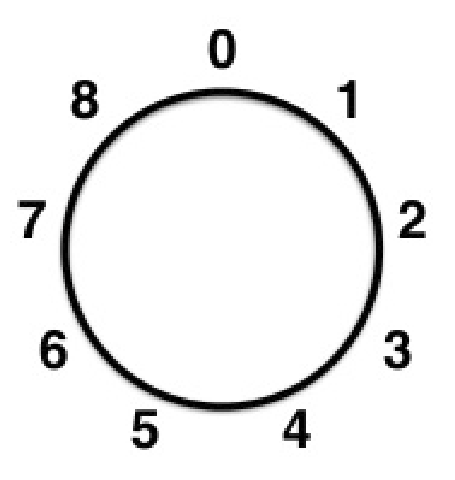 |
Act II
A Brief Encounter with Private-Key Cryptography
A Brief Encounter with Private-Key Cryptography
Big Fact: Modular arithmetic allows us to perform mathematical operations on the alphabet!
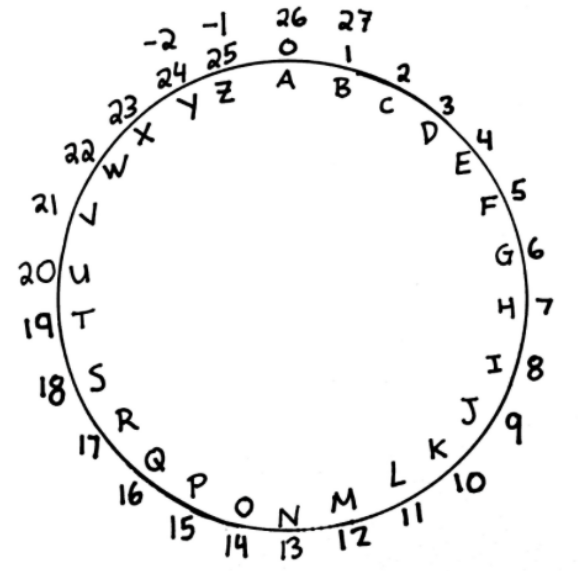
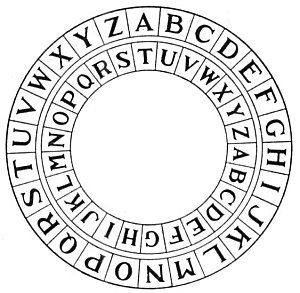
Big Fact: Modular arithmetic allows us to perform mathematical operations on the alphabet!


The Caesar Cipher
To encrypt a letter $p$, shift it to the left or right by some number of spaces $e$ using our decoder pin:

Big Question: Suppose we received the encrypted message $\mbox{AXEI}.$ How would we decrypt it?
The Caesar Cipher
To decrypt a letter $c$, shift it to the left or right by some number of spaces $d$ in the reverse direction of the encryption key $e$:

The Caesar Cipher
To decrypt a letter $c$, shift it to the left or right by some number of spaces $d$ in the reverse direction of the encryption key $e$:

Other Schemes: Affine Cipher $$ p \rightarrow a \cdot p+e \equiv c \,\,(\mbox{mod } 26) $$ where our key is an ordered pair $(a,e)$ where $a$ and $26$ have no common prime factors.
Example: With $(a,e)=(3,19),$ $$ \begin{array}{lcc} \mbox{H} = 7 &\rightarrow & 3 \cdot 7+19 \equiv 14 = \mbox{O}\\ \mbox{E} = 4 &\rightarrow& 3 \cdot 4+19 \equiv 5 = \mbox{F}\\ \mbox{L} = 11 &\rightarrow& 3 \cdot 11+19 \equiv 0 = \mbox{A}\\ \mbox{P} = 15 &\rightarrow & 3 \cdot 15+19 \equiv 12 = \mbox{M}\\ \end{array} $$
Big Problem
The Caesar and Affine Ciphers share a key weakness. Can you spot it?
Frequency Analysis
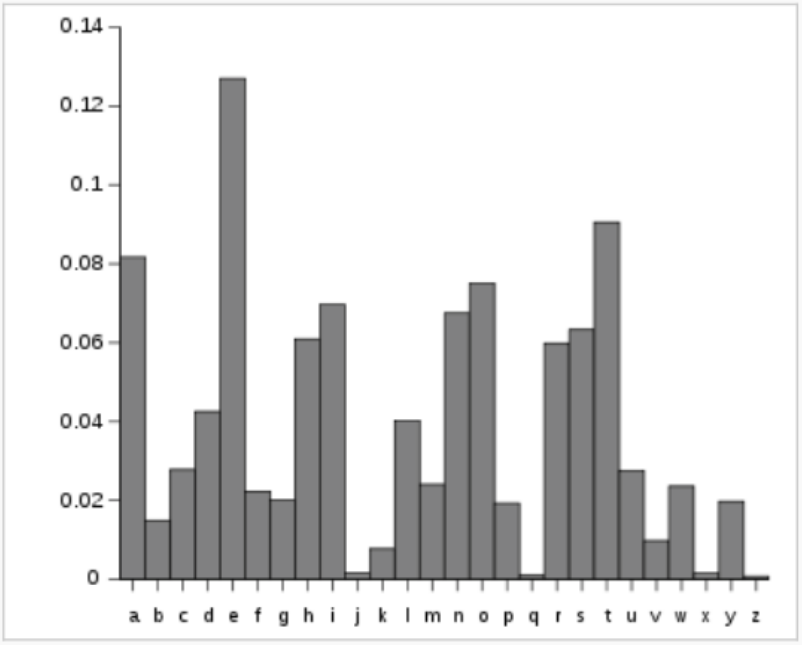
Other Schemes: Vigenère Cipher $$ \left[ \begin{array}{c} p_1 \\ p_2 \\ \vdots\\ p_n \end{array} \right]\rightarrow \left[ \begin{array}{c} p_1+e_1 \\ p_2+e_2 \\ \vdots\\ p_n+e_n \end{array} \right] \equiv \left[ \begin{array}{c} c_1 \\ c_2\\ \vdots\\ c_n \end{array} \right] \,\,(\mbox{mod } 26) $$ Where our encryption key is an $n$-letter "word" $(e_1,e_2,\ldots, e_n).$
Example: With key word $(e_1,e_2,e_3,e_4)=(\mbox{S},\mbox{O},\mbox{O},\mbox{N})=(18,14,14,13),$ $$ \left[ \begin{array}{c} \mbox{H} \\ \mbox{E} \\ \mbox{L} \\ \mbox{P} \end{array} \right] = \left[ \begin{array}{c} 7 \\ 4 \\ 11 \\ 15 \end{array} \right] \rightarrow \left[ \begin{array}{c} \mbox{H}+\mbox{S} \\ \mbox{E}+\mbox{O} \\ \mbox{L}+\mbox{O}\\ \mbox{P}+\mbox{N} \end{array} \right] = \left[ \begin{array}{c} 7+18 \\ 4+14 \\ 11+14\\ 15+13 \end{array} \right] \equiv \left[ \begin{array}{c} 25 \\ 18\\ 25\\ 2 \end{array} \right] = \left[ \begin{array}{c} \mbox{Z} \\ \mbox{S}\\ \mbox{Z}\\ \mbox{C} \end{array} \right] \,\,(\mbox{mod } 26) $$
Bonus Example: The key word doesn't necessarily need to be the same length as the message.
With key word $(e_1,e_2)=(\mbox{M},\mbox{E})=(12,4),$ we can encrypt in "blocks" of length $2$: $$ \left[ \begin{array}{c} \mbox{H} \\ \mbox{E} \\ \mbox{L} \\ \mbox{P} \end{array} \right] = \left[ \begin{array}{c} 7 \\ 4 \\ 11 \\ 15 \end{array} \right] \rightarrow \left[ \begin{array}{c} \mbox{H}+\mbox{M} \\ \mbox{E}+\mbox{E} \\ \mbox{L}+\mbox{M}\\ \mbox{P}+\mbox{E} \end{array} \right] = \left[ \begin{array}{c} 7+12 \\ 4+4 \\ 11+12\\ 15+4 \end{array} \right] \equiv \left[ \begin{array}{c} 19 \\ 8\\ 23\\ 19 \end{array} \right] = \left[ \begin{array}{c} \mbox{T} \\ \mbox{I}\\ \mbox{X}\\ \mbox{T} \end{array} \right] \,\,(\mbox{mod } 26) $$
Other Schemes: Hill Cipher $$ \left[ \begin{array}{c} p_1 \\ p_2 \\ \vdots\\ p_n \end{array} \right]\rightarrow \left[ \begin{array}{cccc} e_{11} & e_{12} & \cdots & e_{1n}\\ e_{21} & e_{22} & \cdots & e_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ e_{n1} & e_{n2} & \cdots & e_{nn}\\ \end{array} \right] \left[ \begin{array}{c} p_1 \\ p_2\\ \vdots\\ p_n \end{array} \right] \equiv \left[ \begin{array}{c} c_1 \\ c_2\\ \vdots\\ c_n \end{array} \right] \,\,(\mbox{mod } 26) $$ The encryption key is the above $n \times n$ matrix which we assume has a determinant of $1$ modulo $26.$
Example: In blocks of $2,$ our message becomes $\,\,\,\,\mbox{H}\mbox{E}\,\,\,\,\mbox{L}\mbox{P}$ $$ \left[ \begin{array}{c} \mbox{H} \\ \mbox{E} \\ \end{array} \right] = \left[ \begin{array}{c} 7 \\ 4 \\ \end{array} \right] \rightarrow \left[ \begin{array}{cc} 5 & 3\\ 1 & 6\\ \end{array} \right] \left[ \begin{array}{c} 7 \\ 4\\ \end{array} \right] = \left[ \begin{array}{c} 5 \cdot 7+3 \cdot 4 \\ 1 \cdot 7+6 \cdot 4\\ \end{array} \right] \equiv \left[ \begin{array}{c} 21 \\ 5\\ \end{array} \right] = \left[ \begin{array}{c} \mbox{V} \\ \mbox{F} \\ \end{array} \right] \,\,(\mbox{mod } 26) $$ $$ \left[ \begin{array}{c} \mbox{L} \\ \mbox{P} \\ \end{array} \right] = \left[ \begin{array}{c} 11 \\ 15 \\ \end{array} \right] \rightarrow \left[ \begin{array}{cc} 5 & 3\\ 1 & 6\\ \end{array} \right] \left[ \begin{array}{c} 11 \\ 15\\ \end{array} \right] = \left[ \begin{array}{c} 5 \cdot 11+3 \cdot 15 \\ 1 \cdot 11+6 \cdot 15\\ \end{array} \right] \equiv \left[ \begin{array}{c} 22 \\ 23\\ \end{array} \right] = \left[ \begin{array}{c} \mbox{X} \\ \mbox{Y} \\ \end{array} \right] \,\,(\mbox{mod } 26) $$ The encrypted message is then $\mbox{VFXY}.$
Bonus Example: To decrypt the message $\mbox{VFXY}$ we again break our message into blocks of $2$: $\,\,\,\,\mbox{V}\mbox{F}\,\,\,\,\mbox{X}\mbox{Y}.$ Then multiply by the modulo-$26$ inverse of the encrypting matrix. $$ \left[ \begin{array}{c} \mbox{V} \\ \mbox{F} \\ \end{array} \right] = \left[ \begin{array}{c} 21 \\ 5 \\ \end{array} \right] \rightarrow \left[ \begin{array}{cc} 6 & 23\\ 25 & 5\\ \end{array} \right] \left[ \begin{array}{c} 21 \\ 5\\ \end{array} \right] = \left[ \begin{array}{c} 6 \cdot 21+23 \cdot 5 \\ 25 \cdot 21+5 \cdot 5\\ \end{array} \right] \equiv \left[ \begin{array}{c} 7 \\ 4\\ \end{array} \right] = \left[ \begin{array}{c} \mbox{H} \\ \mbox{E} \\ \end{array} \right] \,\,(\mbox{mod } 26) $$ $$ \left[ \begin{array}{c} \mbox{X} \\ \mbox{Y} \\ \end{array} \right] = \left[ \begin{array}{c} 22 \\ 23 \\ \end{array} \right] \rightarrow \left[ \begin{array}{cc} 6 & 23\\ 25 & 5\\ \end{array} \right] \left[ \begin{array}{c} 22 \\ 23\\ \end{array} \right] = \left[ \begin{array}{c} 6 \cdot 22+23 \cdot 23 \\ 25 \cdot 22+5 \cdot 23\\ \end{array} \right] \equiv \left[ \begin{array}{c} 11 \\ 25\\ \end{array} \right] = \left[ \begin{array}{c} \mbox{L} \\ \mbox{P} \\ \end{array} \right] \,\,(\mbox{mod } 26) $$
Fact: Among their many limitations, all of the above schemes have a particular drawback which makes them unsuitable for publicly exchanging information in our modern age...
...both the sender and receiver of a message must have the encryption/decryption key.
All of the encryption/decryption schemes we have considered so far are examples of private-key cryptosystems.
Observation: knowing how a sender encrypted a message tells us how to decrypt it.
Act II Cliffhanger
Is there a scheme where knowing how a message was encrypted doesn't tell us how to decrypt it?
Act III
Modular Arithmetic Redux: Fermat's Little Theorem
Modular Arithmetic Redux: Fermat's Little Theorem
Fermat's Little Theorem
If a prime $p$ does not divide $a$, then $$a^{p-1} \equiv 1 \,\,(\mbox{mod } p).$$

Examples
$$4^{2} \equiv \,\,\,\,(\mbox{mod } 3).$$ $$8^{2} \equiv \,\,\,\,(\mbox{mod } 3).$$ $$2^{4} \equiv \,\,\,\,(\mbox{mod } 5).$$ $$3^{4} \equiv \,\,\,\,(\mbox{mod } 5).$$ $$2^{6} \equiv \,\,\,\,(\mbox{mod } 7).$$ $$2^{10} \equiv \,\,\,\,(\mbox{mod } 11).$$
A Slight Generalization
If primes $p$ and $q$ do not divide $a$, then $$a^{(p-1)(q-1)} \equiv 1 \,\,(\mbox{mod } pq).$$
A Broader Generalization: Euler's Theorem
If the natural numbers $n$ and $a$ have no prime factors in common, then $$a^{\varphi(n)} \equiv 1 \,\,(\mbox{mod } n).$$ The function $\varphi(n)$ is Euler's Totient function which is the number of natural numbers less than $n$ which have no prime factors in common with $n.$

If primes $p$ and $q$ do not divide $a$, and $e$ and $d$ are two numbers such that $${ed} \equiv 1 \,\,(\mbox{mod } (p-1)(q-1)),$$ then $$a^{ed} \equiv a \,\,(\mbox{mod } pq).$$
Act IV
The World's First Public-Key Cryptographic Scheme: RSA
The World's First Public-Key Cryptographic Scheme: RSA
The Situash: Bob would like to receive a secret message from Alice.
Moreover, Bob would like to be able to make the method of encryption public so that anyone could send him an encrypted message, but only Bob can decrypt the message.
Question: Is this even possible?
RSA System Basics
Step 1: Bob finds two large primes $p$ and $q$ and computes their product $n=pq.$
Step 2: Bob then finds two numbers $e$ and $d$ such that $${ed} \equiv 1 \,\,(\mbox{mod } (p-1)(q-1)).$$ Step 3: Bob publishes the key $(e,n)$ where $e$ is an encryption exponent and $n.$
Step 4: Alice encrypts the message $a$ by computing $a^e \,\,(\mbox{mod } n)$, and sends this to Bob.
Step 5: Bob takes the remainder of $a^{e}$ upon division by $n$ and raises it to the power of his decryption exponent $d$ so that $$(a^e)^d \equiv a^{ed} \equiv a \,\,(\mbox{mod } n).$$
Example
Step 1: Bob chooses two "large" primes $p=53$ and $q=59$ and computes $n=pq=3127.$
Step 2: Bob then finds two numbers $e$ and $d$ such that $ed \equiv 1 \,\,(\mbox{mod } 3016).$ For this example, $e=7$ and $d=431$ will do the trick.
Step 3: Bob publishes the encryption key $(7,3127).$
Step 4: Alice encrypts the message $\mbox{HELP}$ in blocks of 2: $0704^7 \equiv 254 \,\,(\mbox{mod } 3127)$ and $1115^7 \equiv 1612 \,\,(\mbox{mod } 3127)$ and sends the message $0254\,\,1612$ to Bob.
Step 5: Bob uses his decrypting exponent $431$ to decode the message: $254^{431} \equiv 704 \,\,(\mbox{mod } 3127)$ and $1612^{431} \equiv 1115 \,\,(\mbox{mod } 3127)$ and recovers the message $0704 \,\, 1612,$ i.e., $\mbox{HELP}.$
Huge Question #1: How did Bob compute $254^{431} \equiv 704 \,\,(\mbox{mod } 3127)?$
Modular Exponentiation $$431=2^8+2^7+2^5+2^3+2^2+2+1$$ $$ \begin{array}{l} 254^2 \equiv 1976 \,\,(\mbox{mod } 3127)\\ 254^4 \equiv 1976^2 \equiv 2080\,\,(\mbox{mod } 3127) \\ 254^8 \equiv 2080^2 \equiv 1759\,\,(\mbox{mod } 3127) \\ 254^{16} \equiv 1759^2 \equiv 1478\,\,(\mbox{mod } 3127) \\ 254^{32} \equiv 1478^2 \equiv 1838\,\,(\mbox{mod } 3127) \\ 254^{64} \equiv 1838^2 \equiv 1084\,\,(\mbox{mod } 3127) \\ 254^{128} \equiv 1084^2 \equiv 2431\,\,(\mbox{mod } 3127) \\ 254^{256} \equiv 2431^2 \equiv 2858\,\,(\mbox{mod } 3127) \\ \end{array} $$ $$ \begin{array}{l} 254^{431} \equiv 254^{2^8+2^7+2^5+2^3+2^2+2+1} \equiv 254^{2^8} \cdot 254^{2^7} \cdot 254^{2^5} \cdot 254^{2^3} \cdot 254^{2^2} \cdot 254^{2} \cdot 254 ^1\\ \equiv 254^{256} \cdot 254^{128} \cdot 254^{32} \cdot 254^{8} \cdot 254^{4} \cdot 254^{2} \cdot 254 ^1\\\ \equiv 2858 \cdot 2431 \cdot 1838 \cdot 1759 \cdot 2080 \cdot 1976 \cdot 254 \equiv 704 \,\,(\mbox{mod } 3127)\\ \end{array} $$
Huge Question #2: What makes this scheme secure against an eavesdropper?

The security of RSA rests on the following fact:
Multiplying two numbers, even huge numbers, is child's play to a computer, but unmultiplying two numbers (i.e., factoring) can be intractable.
For example, factor this product of two large primes $p$ and $q$: $$\scriptsize{n=1522605027922533360535618378132637429718068114961380688657908494580122963258952897654000350692006139}$$ The eavesdropper knows $e$ and $n,$ but they must also know primes $p$ and $q$ in order to find the decrypting exponent $d$: $$ed \equiv 1 \,\,(\mbox{mod } (p-1)(q-1)).$$ Good luck finding $p$ and $q!$

In Case You're Curious:
$$\scriptsize{p \times q =37975227936943673922808872755445627854565536638199 \times 40094690950920881030683735292761468389214899724061}$$
Huge Question #3: Where did Bob find such large primes?
Finding Large Prime Numbers: Miller's Test
Suppose we suspect that some odd natural number $n$ is prime. How do we test this?
Theorem: Suppose $n-1=2^sd$ and let $a$ be less than $n.$
If $a^{d} \not \equiv 1 \,\,(\mbox{mod } n)$ and $a^{2^s d} \not\equiv -1 \,\, (\mbox{mod } n),$ then $n$ is not prime.
In the above case, we say that $n$ fails Miller's test.
Otherwise, $n$ passes Miller's test.
Finding Large Prime Numbers: Miller's Test
Suppose we suspect that some odd natural number $n$ is prime. How do we test this?
Theorem: Choose a random natural number $a$ less than $n$ and perform Miller's with $a$ serving as the base.
Then the probability that $n$ passes Miller's test given that $n$ is not prime is less than $\displaystyle \frac{1}{4}.$
Example
Suppose that we want to test if $n=37975227936943673922808872755445627854565536638199$ is prime.
Randomly choose 100 bases $a$ less than $n$ and perform Millers test for each base.
Suppose it passes Miller's test for each of these 100 randomly-chosen bases.
If $n$ were not prime, the probability of this happening by chance alone is less than $\frac{1}{4^{100}}\approx \frac{1}{1.6\times 10^{60}}.$
Act V
Dénouement
Dénouement
Public-Key Cryptography Makes Modern Life Possible.
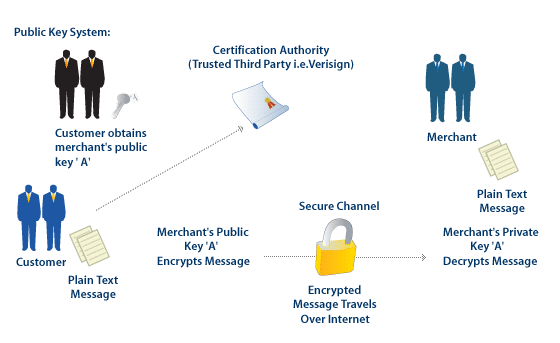
Olde Theorems, Modern Applications
Fermat's Little Theorem is over 350 years old.

Such cases stand as a testament that one should be quite wary of deeming the pursuit of any idea, even if only for its own charm and beauty, a worthless endeavor.
Thank You!
Take two large prime numbers, $q$ and $p.$
Find the product $n,$ and the totient $\varphi.$
If $e$ and $\varphi$ have GCD one
and $d$ is $e$'s inverse, then you're done!
For sending $m$ raised to the $e$
reduced mod $n$ gives secre-$c.$
Take two large prime numbers, $q$ and $p.$
Find the product $n,$ and the totient $\varphi.$
If $e$ and $\varphi$ have GCD one
and $d$ is $e$'s inverse, then you're done!
For sending $m$ raised to the $e$
reduced mod $n$ gives secre-$c.$