MTH 101: Cryptography
~OR~
How to Pass Notes Your Teacher Can't Read to the Rest of the Class
Benjamin V. Holt
College $101$
March $20$th, $2025$
~OR~
How to Pass Notes Your Teacher Can't Read to the Rest of the Class
Benjamin V. Holt
College $101$
March $20$th, $2025$
Cryptography is an ancient and modern practice.





Part I
Modular Arithmetic
Modular Arithmetic
Modular Arithmetic
Modular arithmetic is remainder arithmetic.
Two numbers are "equal" if they have the same remainder when dividing by a fixed number called the modulus.
For example, $19$ and $10$ have the same remainder when we divide both by $9.$
We may write the above as $19 \equiv 10 \equiv 1 \,\,(\mbox{mod } 9).$
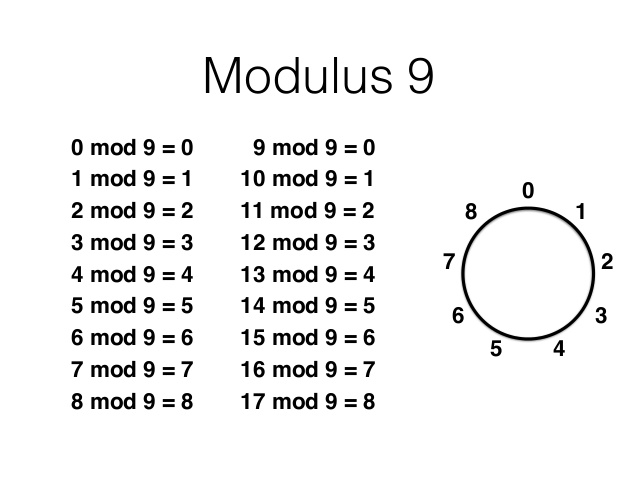
Modular Arithmetic
If you can answer the following question, then you are already familiar with one example of modular arithmetic:
Suppose it's $11$ am. What time will it be in $4$ hours?
Modular Arithmetic
Time to leave!

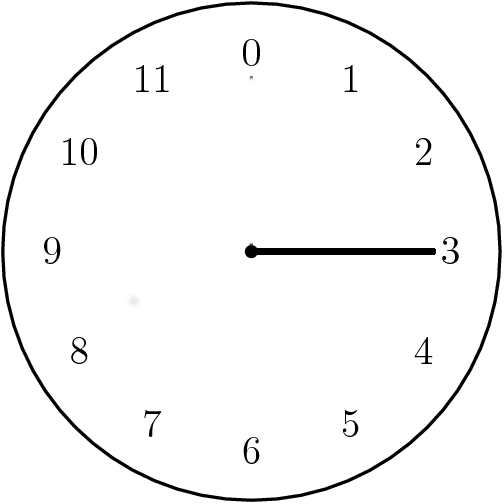


We just performed arithmetic modulo $12$: $$11+4 \equiv 15 \equiv 3 \,\,(\mbox{mod } 12).$$
Modular Arithmetic: Examples.
| $7+9 \equiv \,\,\,\,\,\,\,\,(\mbox{mod } 12)$ | $7-9 \equiv \,\,\,\,\,\,\,\,(\mbox{mod } 12)$ |  |
| $3+8 \equiv \,\,\,\,\,\,\,\,(\mbox{mod } 9)$ | $3-8 \equiv \,\,\,\,\,\,\,\,(\mbox{mod } 9)$ | 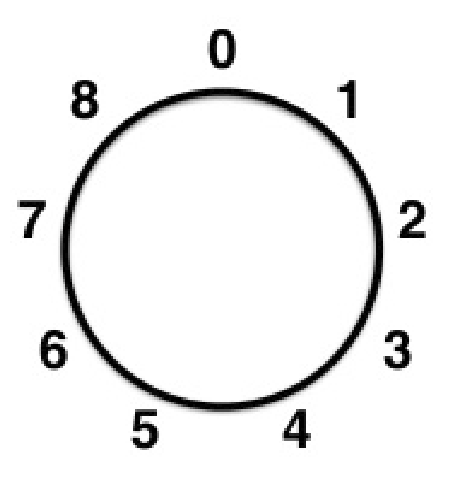 |
Part II
Cryptography Basics
Cryptography Basics
Big Fact: Modular arithmetic allows us to perform mathematical operations on the alphabet!
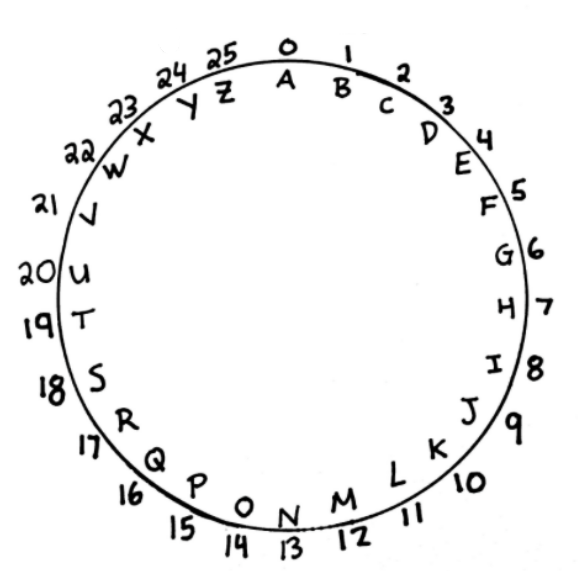

Big Fact: Modular arithmetic allows us to perform mathematical operations on the alphabet!

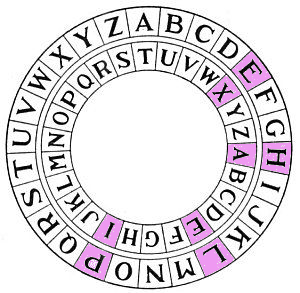
The Caesar Cipher
To encrypt a letter $p$, shift it to the left or right by some number of spaces $e$ using our decoder pin:

Big Question
Suppose we received the encrypted message $\mbox{AXEI}.$
How would we decrypt it?
Big Answer
Simply use modular arithmetic; to decrypt, simply subtract $\mbox{T}=19.$
For example, $$\mbox{A} = 0 \rightarrow \mbox{A}-\mbox{T}=0-19 \equiv 26-19 \equiv 7 = \mbox{H}.$$


The Caesar Cipher


The Caesar Cipher


Your Turn!
It's time to get into groups!
Mission #$1:$
The following is Part $1$ of a super-secret message encrypted by using $\mbox{K}$ as our shift letter. $$\color{blue}{\mbox{ZBSJOCKBORSN}}\color{magenta}{\mbox{NOXSXDROBYYW}}$$
Decrypt this message!


Big Problem
Although your English teacher might not be able to make heads or tails of your encrypted notes, the Caesar cipher a huge weakness.
In your groups, discuss what you think that weakness is?
Frequency Analysis
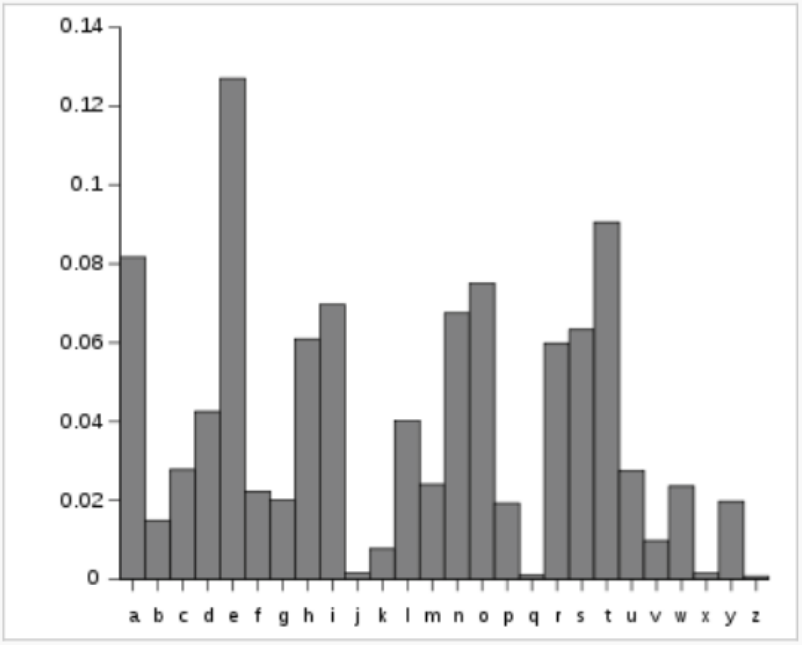
Mission #$2:$ What shift letter was used to encrypt the following message?
The following is Part $2$ of a super-secret message encrypted by an UNKNOWN shift letter. $$\mbox{AOLWYPGLZHYLZTHSSHUKZDLLA}$$
We'll decrypt the message together when you find the correct shift letter.


Historical Fact
Even though the Caesar Cipher is relatively easy to crack, Julius Caesar really did use it. According to the Roman historian Suetonius, he often used $\mbox{D}$ as the shift letter.

Another Scheme: Vigenère Ciphers
Vigenère Ciphers use a key word rather than a key letter.
Example: With key word $(\mbox{S},\mbox{O},\mbox{O},\mbox{N})=(18,14,14,13),$ $$ \left[ \begin{array}{c} \mbox{H} \\ \mbox{E} \\ \mbox{L} \\ \mbox{P}\\ \mbox{M} \\ \mbox{E} \\ \mbox{O}\\ \mbox{U} \\ \mbox{T} \end{array} \right] = \left[ \begin{array}{c} 7 \\ 4 \\ 11 \\ 15 \\ 12 \\ 4 \\ 14\\ 20\\ 19 \end{array} \right] \rightarrow \left[ \begin{array}{c} \mbox{H}+\mbox{S} \\ \mbox{E}+\mbox{O} \\ \mbox{L}+\mbox{O}\\ \mbox{P}+\mbox{N}\\ \mbox{M}+\mbox{S}\\ \mbox{E}+\mbox{O}\\ \mbox{O}+\mbox{O}\\ \mbox{U}+\mbox{N}\\ \mbox{T}+\mbox{S}\\ \end{array} \right] = \left[ \begin{array}{c} 7+18 \\ 4+14 \\ 11+14\\ 15+13\\ 12+18\\ 4+14\\ 14+14\\ 20+13\\ 19+18\\ \end{array} \right] \equiv \left[ \begin{array}{c} 25 \\ 18\\ 25\\ 2\\ 4\\ 18\\ 2\\ 7\\ 11 \end{array} \right] = \left[ \begin{array}{c} \mbox{Z} \\ \mbox{S}\\ \mbox{Z}\\ \mbox{C}\\ \mbox{E} \\ \mbox{S}\\ \mbox{C}\\ \mbox{H}\\ \mbox{L} \end{array} \right] \,\,(\mbox{mod } 26) $$
Mission #$3:$ Claim your prize!
The next slide contains an encrypted message which will reveal the location(s) of the prizes.
Are you ready?
Mission #$3:$ Claim your prize!
The following is a location that was encrypted by using a Vigenère Cipher with a key word. $$\mbox{QRKJTPTSTRSVZVLXKMASPIL}$$

Put you hacker hats on, grab your phones, and decrypt this message!
While you enjoy your prizes, let's talk about...
Part III
Public-Key Cryptography
Public-Key Cryptography
Fact
The Caesar, Vigenère, and even the ENIGMA ciphers (used by Germany in WWII) have a particular drawback which makes them unsuitable for publicly exchanging information in our modern age...
...both the sender and receiver of a message must have the encryption/decryption key.
All of the encryption/decryption schemes we have considered so far are examples of private-key cryptosystems.
Observation: knowing how a sender encrypted a message tells us how to decrypt it.
Big Question
Is there an encryption scheme where knowing how a message was encrypted doesn't tell us how to decrypt it?
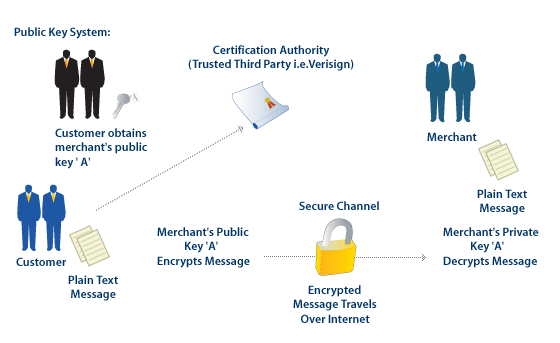
The Situash: Bob would like to receive a secret message from Alice.
Moreover, Bob would like to be able to make the method of encryption public so that anyone could send him an encrypted message, but only Bob can decrypt the message.
Question: Is this even possible?
RSA System Basics
Step 1: Bob finds two large primes $p$ and $q$ and computes their product $n=pq.$
Step 2: Bob then finds two numbers $e$ and $d$ such that $${ed} \equiv 1 \,\,(\mbox{mod } (p-1)(q-1)).$$ Step 3: Bob publishes the key $(e,n)$ where $e$ is an encryption exponent and $n.$
Step 4: Alice encrypts the message $a$ by computing $a^e \,\,(\mbox{mod } n)$, and sends this to Bob.
Step 5: Bob takes the remainder of $a^{e}$ upon division by $n$ and raises it to the power of his decryption exponent $d$ so that $$(a^e)^d \equiv a^{ed} \equiv a \,\,(\mbox{mod } n).$$
Fermat's Little Theorem
If a prime $p$ does not divide $a$, then $$a^{p-1} \equiv 1 \,\,(\mbox{mod } p).$$

Example
Step 1: Bob chooses two "large" primes $p=53$ and $q=59$ and computes $n=pq=3127.$
Step 2: Bob then finds two numbers $e$ and $d$ such that $ed \equiv 1 \,\,(\mbox{mod } 3016).$ For this example, $e=7$ and $d=431$ will do the trick.
Step 3: Bob publishes the encryption key $(7,3127).$
Step 4: Alice encrypts the message $\mbox{HELP}$ in blocks of 2: $0704^7 \equiv 254 \,\,(\mbox{mod } 3127)$ and $1115^7 \equiv 1612 \,\,(\mbox{mod } 3127)$ and sends the message $0254\,\,1612$ to Bob.
Step 5: Bob uses his decrypting exponent $431$ to decode the message: $254^{431} \equiv 704 \,\,(\mbox{mod } 3127)$ and $1612^{431} \equiv 1115 \,\,(\mbox{mod } 3127)$ and recovers the message $0704 \,\, 1612,$ i.e., $\mbox{HELP}.$
Huge Question: What makes this scheme secure against an eavesdropper?

The security of RSA rests on the following fact:
Multiplying two numbers, even huge numbers, is child's play to a computer, but unmultiplying two numbers (i.e., factoring) is really hard.
For example, factor this product of two large primes $p$ and $q$: $$\scriptsize{n=1522605027922533360535618378132637429718068114961380688657908494580122963258952897654000350692006139}$$ The eavesdropper knows $e$ and $n,$ but they must also know primes $p$ and $q$ in order to find the decrypting exponent $d$: $$ed \equiv 1 \,\,(\mbox{mod } (p-1)(q-1)).$$ Good luck finding $p$ and $q!$

In Case You're Curious:
$$\scriptsize{p \times q =37975227936943673922808872755445627854565536638199 \times 40094690950920881030683735292761468389214899724061}$$
Public-Key Cryptography Makes Modern Life Possible.
Olde Theorems, Modern Applications
Fermat's Little Theorem is over $350$ years old.

Such cases stand as a testament that we never know when an idea will turn out to be useful.
Thank You!
Take two large prime numbers, $q$ and $p.$
Find the product $n,$ and the totient $\varphi.$
If $e$ and $\varphi$ have GCD one
and $d$ is $e$'s inverse, then you're done!
For sending $m$ raised to the $e$
reduced mod $n$ gives secre-$c.$
Take two large prime numbers, $q$ and $p.$
Find the product $n,$ and the totient $\varphi.$
If $e$ and $\varphi$ have GCD one
and $d$ is $e$'s inverse, then you're done!
For sending $m$ raised to the $e$
reduced mod $n$ gives secre-$c.$